Security and Privacy of Machine Learning
University of Virginiacs6501 Seminar Course, Spring 2018
Coordinator: David Evans
Thanks for a great semester!
Here’s the topics we covered:
Class 1: Intro to Adversarial Machine Learning
Class 2: Privacy in Machine Learning
Class 3: Adversarial Machine Learning
Class 4: Differential Privacy In Action
Class 5: Adversarial Machine Learning in Non-Image Domains
Class 6: Measuring Robustness of ML Models
Class 7: Biases in ML, Discriminatory Advertising
Class 8: Testing of Deep Networks
Class 9: Adversarial Malware Detection
Class 10: Formal Verification Methods
Class 11: Poisoning
This week we discussed poisoning attacks, which differ from previously-discussed attacks in a key way. Instead of finding test instances that the target model misclassifies, a poisoning attack adds “poisoned” instances to the training set, introducing new errors into the model. Below are three papers which discuss interesting work happening in this field.
Poison Frogs!
Ali Shafahi, W. Ronny Huang, Mahyar Najibi, Octavian Suciu, Christoph Studer, Tudor Dumitras, and Tom Goldstein. Poison Frogs! Targeted Clean-Label Poisoning Attacks on Neural Networks. April 2018. arXiv e-print [PDF]
A Simple Clean Label Attack
The paper presents a novel clean-label attack, which restricts the attacker to injecting correctly-classified examples into the victim’s training set. The goal of the attacker is to make the model misclassify a “target” instance, specifically to the same class as some chosen “base” instance. The attack is executed by subtly changing the base instance to display features of the target; this is illustrated in Figure (a) below. Figure (b) shows a simple diagram of the intended effect on the model’s decision boundary. When the model trains, it hopefully overfits on the poisoned instance, thereby allowing the target to be classified incorrectly. The major benefit of this approach is that it is difficult for the victim to detect: since the poisoned data is still labeled correctly, the model’s test accuracy should not change.
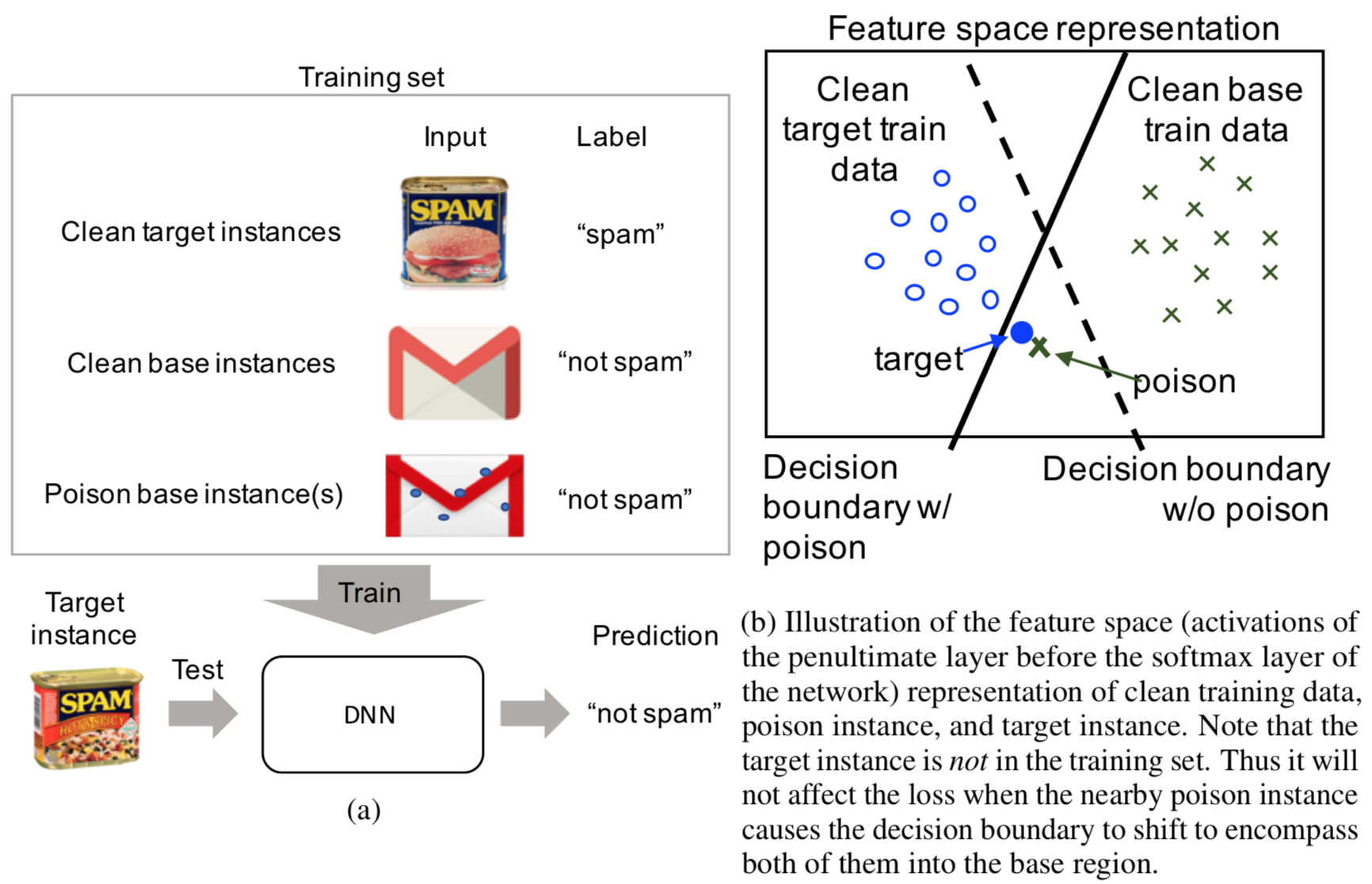
In more formal language, the clean-label attack does this: given a target instance \(t\) and a base instance \(b\), create a poisoned instance \(p\) such that
- \(p\) is humanly-indistinguishable from \(b\) (and is classified the same), and
- the model, after training on a data set that includes \(p\), misclassifies \(t\) to be in the same class as \(b\).
The equivalent optimization problem is
where \(\beta\) represents how closely \(p\) resembles the base instance \(b\). There is a simple algorithm for solving this optimization problem: alternate between “forward steps” to inch closer to \(t\) and “backward steps” to stay close to \(b\).
The clean-label attack works extremely well on transfer learning models, which contain a pre-trained feature extraction network hooked up to a trainable, final classification layer. As an example, the authors created an InceptionV3 model that classified images of dogs and fish. They were able to attack this model a 100% success rate by including just one poisoned image in each attack; furthermore, the target images were misclassified by the model with high confidence:
Watermarking Attack on End-to-End Training
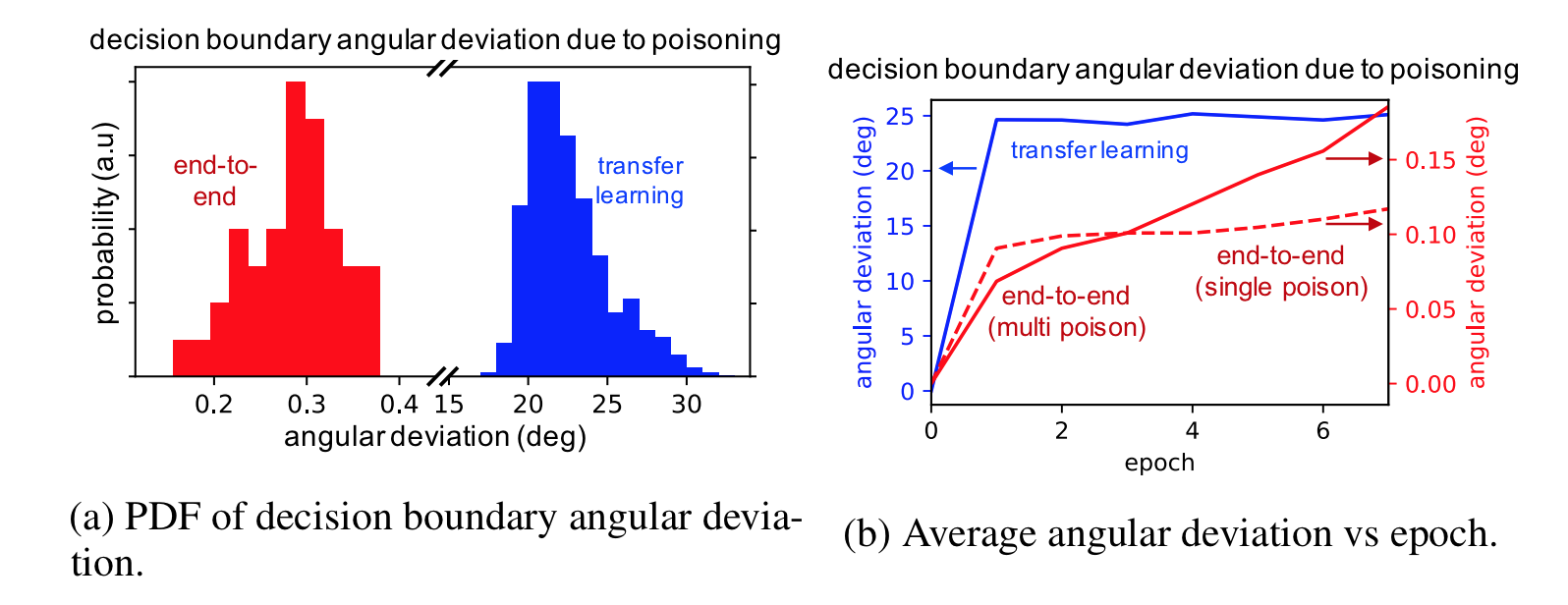
The poisoning attack above is effective when the early feature extraction layers of a network are not retrained (as in transfer learning), but is not as effective when training end-to-end. The figure below shows this effect measured by the angular deviation of the decision boundary. The angular deviation is the angular difference between the decision boundary of a clean and poisoned network. A high angular deviation indicates the poisoning attack was strong, causing the decision boundary to significantly shift. We see that the poisoning attack we’ve discussed does not shift the decision boundary on end-to-end learning nearly as much as it does for transfer learning.
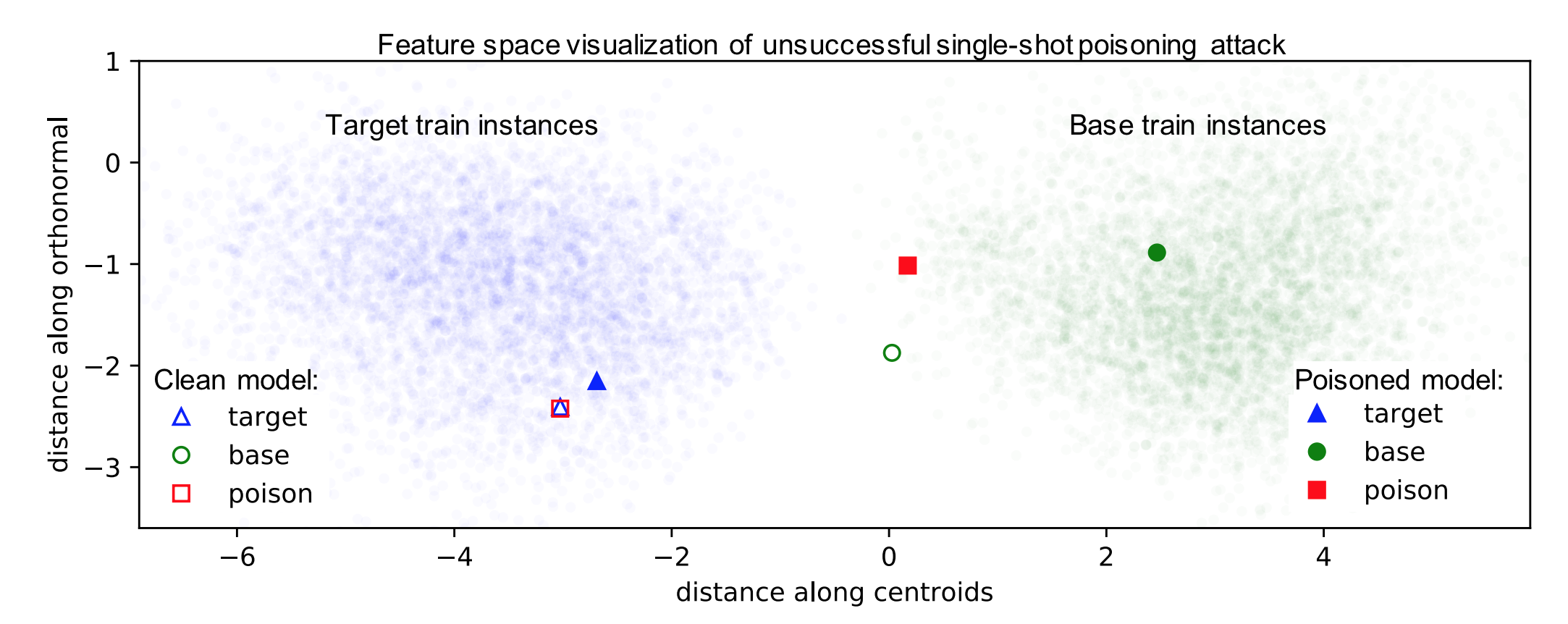
The figure below shows the feature space representations of the target, base, and poison instances in the context of their training data for a single-shot poisoning attack. The clean model shows the target and poison instance overlapping – this indicates the optimization algorithm to find a poison instance works. However, we see that retraining the network separates the poison and target instances and returns the poison instance to the base class.
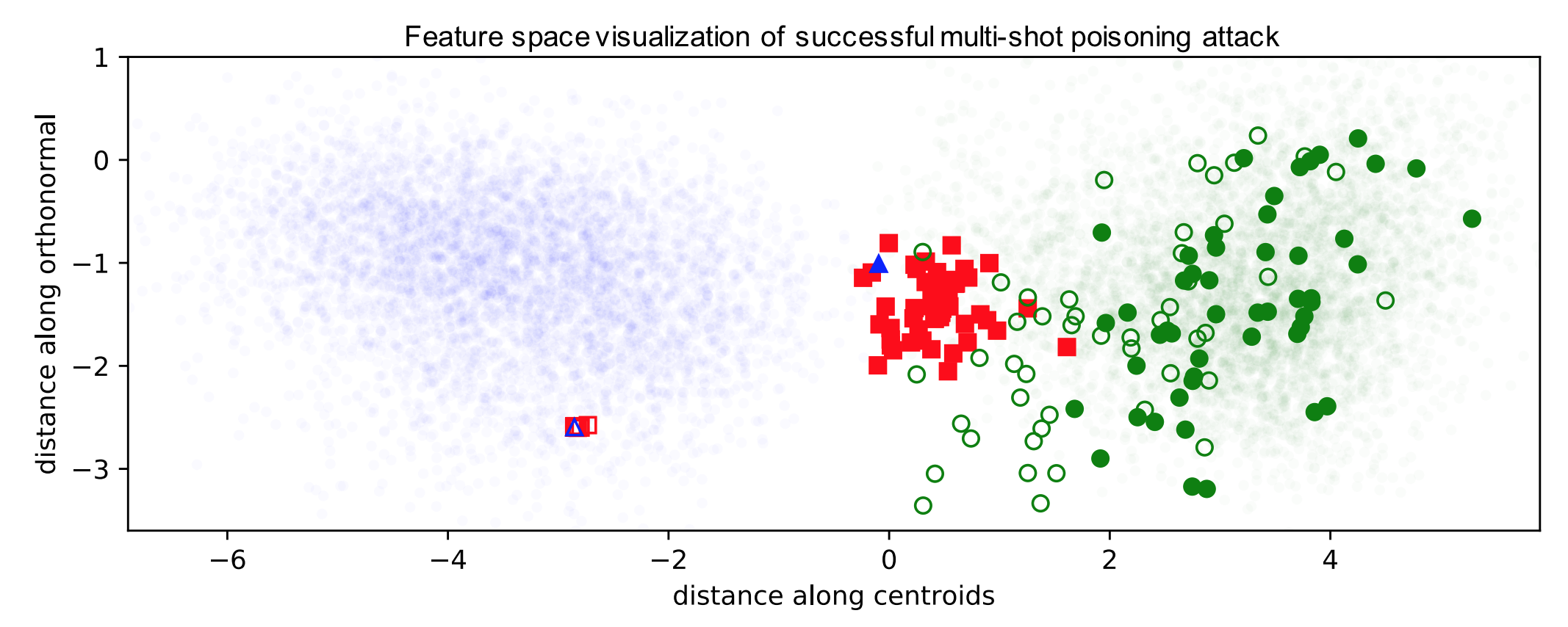
To fix this, the authors use a technique called watermarking. Watermaking blends additional features of the target instance into the poison instance in a way humans can’t notice. In particular, a low opacity watermark of the target instance is added to the poison instances. Watermarks are not noticeable to humans up to 30% opacity. The figure below shows how constructing 50 poison instances from 50 random base instances casuses the target instances to be pulled out of the target feature space into the base class feature space, resulting in incorrect classifications.
We see below 60 images of dogs with watermarks of birds at 30% opacity. These poison instances successfully cause a target image of a bird to get misclassified as a dog with end-to-end training.
The authors found that targeting outlier instances has a 17% higher success rate. Since these targets lie far from other training samples in their class, they are close to the decision boundary, and it is therefore easier to flip their class label. Additionally, the authors found that the attack success rate was higher when more poison instances were included in the retraining and when the watermark had a higher opacity.
Poisoning Regression Learning
Matthew Jagielski, Alina Oprea, Battista Biggio, Chang Liu, Cristina Nita-Rotaru and Bo Li. Manipulating Machine Learning: Poisoning Attacks and Countermeasures for Regression Learning. April 2018. arXiv e-print [PDF] (IEEE Symposium on Security and Privacy 2018)
It is well understood that machine learning models are easy to be manipulated by smart attackers. There are both test-time evasion attacks and training-time data poisoning attacks, so studying and understanding these potential risks is beneficial for the application of machine learning in security critical domains.
In this paper, the authors studied the specific problem of training a data poisoning attack on linear regression models and subsequently proposed an effective defensive strategy.
A linear regression is defined as
And the loss function being optimized during the training time is the mean-squared error (MSE), which is defined as:
MSE is used here as the result of linear regression and is a continuous value, while a traditional classification task outputs discrete categorical values. The term \(\Omega(\mathbf{w})\) denotes the regularization terms. When we take different norms, it corresponds to different regularization functions. (\(L\)2-norm corresponds to ridge regression, \(L\)1-norm to LASSO regression, and Elastic-net Regression takes the linear combination of \(L\)1-norm and \(L\)2-norm).
Optimization-based Poisoning Attack
The attack aims to corrupt the machine learning in the training phase by introducing noisy training data points such that predictions at test time will be influenced. The author considered both the white-box and black-box attack. White-box attack means the attacker is aware of all the information including training dataset, feature values, training algorithm and trained parameters. In the black-box setting, the training dataset is assumed to be unknown. With all these described, we arrive at the following formulation regarding training data poisoning attack:
where \(\mathbf{\theta}{p}^{*}\) is the model parameter obtained by training the model on poisoned training dataset. \(D{tr}\) denotes unpoisoned training data, and \(D_{p}\) are the poisoned training data, which typically takes around \(10%\) of the clean training data. \(W(D^{'},\mathbf{\theta}_{p}^{*})\) is the loss function defined on the test (or validation) dataset \(D^{'}\), which is free from the poisoning attacks. (Sorry, can’t fix the mathjax typesetting for this paragraph; please check the original paper if confused.)
Note that this is a bilevel optimization problem and is different from the traditional optimization we know, in that the constraint itself is an optimization problem. Also, the parameter \(\theta_{p}^{*}\) depends implicitly on the poisoned training dataset \(D_{p}^{*}\).
To optimize the above problem with respect to a set of data points \(D_{p}\), the approach is to optimize each instance \(\mathbf{x}_{c}\) in the set \(D_{p}\). With this, the authors apply gradient descent algorithms to find an optimal \(\mathbf{x}_c\) that can maximize the loss function \(W(\cdot)\). The gradient can be calculated as below:
The calculation of first term is non-trivial as there is an implicit dependence of \(\mathbf{\theta}\) and \(\mathbf{x}_c\). With some tricks played by KKT equilibrium conditions, the author arrived at this equation:
Combining the above two, we are able to approximately compute the gardient and update \(\mathbf{x}c\). Notably, unlike previous papers on training data poisoning attacks on classifiers, the problem setting of this paper is in linear regression, and the authors further propose to optimize both the data point \(\mathbf{x}c\) and its response variable \(y_c\). Hence, a new variable \(\mathbf{z}{c}= (\mathbf{x}{c},y_{c})\) is introduced to replace \(\mathbf{x}_c\). Details of the gradient of \(W\) with respect to variable \(\mathbf{z}_{c}\) can be referred from equation (14) and equation (4).
Statistical-based Poisoning Attack
Statistical Attack contrasts the previous optimization based attack. Statistical attack is computationally efficient and it operates by generating adversarial training points from a multivariate normal distribution with mean and covariance estimated from the training data. Then, the feature values are rounded to corner values and the finally the response value \(y_{c}\) for a given data point \(\mathbf{x}_c\) is rounded to the boundary value (either 1 or 0). As can be seen from the description, it is computationally effective but less accurate than the optimization based method.
TRIM algorithm
This is the defense method proposed by the author to tackle the two above-mentioned attack strategies. The TRIM algorithm operates by iteratively estimating the regression parameters while at the same time training on a subset of points with lowest residuals in each iteration. Here, residual means error in a result. For example, error is taken with respect to \(\mathbf{x}_c\) while residual with taken with respect to \(f(\mathbf{x})\). The intuitive understanding of this algorithm is in that, majority of the training points are non-corrupted and poisoned data points typically exhibit larger outlier behavior. If poisoned data points do not have outlier behavior, then its effect on regression task is minimized and hence can be considered as less harmful. The TRIM algorithm actually provides a solution to the following optimization problem:
The optimization problem above intuitively represents that we optimize the regression parameter \(\theta\) and the subset of points with smallest residuals at the same time. This problem is computionally challenging as a simple approach of enumarating all possible subsets of \(I\) of size \(n\) is large. Also, the parameter \(theta\) is typically unknown without any prior assumptions (if we know \(\theta\) in advance, we can simply choose \(I\) as a set of \(n\) points with lowest residuals with respect to \(theta\)).
The solution to the challenge above is to alternatively optimize parameter \(\theta\) and \(I\). Specifically, at the begining of iteration \(i\), an estimation of parameter \(\theta\) is obtained based on the current set \(I\). Next, with the selected parameter \(\theta\), the set \(I\) is updated by selecting \(n\) points with lowest residuals with respect to \(\theta\). As for side note, the first iteration, the set \(I\) is initialized with random set of size \(n\). \(theta\) is updated through some initialization technique or prior knowledge.
The theorem 1 in the paper proves that the TRIM terminates in finite number of steps, and hence convergence of the algorithm is guaranteed. The following theorem (theorem 2 in the paper) provides an upper bound on the worst case loss of the regression model under adversarial noise injection.
The left hand side means the loss on clean data (test or validation dataset) with respect to parameters trained on noisy data is upper bounded by fraction \(1 + \frac{\alpha}{1-\alpha}\) with respect to best case training loss on clean data \(D_{tr}\) and parameter \(\theta^{*}\) is obtained by training on the clean dataset. Hence, right hand side actually denotes a ideal-case scenario. Note that, an implicit assumption here is \(D^{''}\) and \(D_{tr}\) follow same distribution. Also, note that \(alpha\) is the fraction of poisoned data points in the training set, which is typically very small.
Experimental Results
In this paper, the author used Health care dataset, Loan Dataset and House pricing dataset, which all are well-suited for regression tasks. The results in this blog only contains results for ridge regression tasks. As shown in the figure below (Fig3 in the paper), the optimization based attack method and statistical attack method proposed in this paper outperform the baseline gradient desend (BGD) method significantly. (BGD is a method adapted from previous attack method on classification task. There are no existing methods on attacking regression models).
As for the defense method, following figure illustrates its effectiveness in face of the attacks described in previous sections. It is obvious that TRIM algorithm (defense method proposed in this paper) outperforms other defense methods significantly. Three other defense methods are from existing works that are suitable for countering the attacks proposed in this paper (RANSAC and Huber from robust statistics and RONI implemented by authors based on this and this).
Conclusion
As a concluding mark, this paper is the first paper to consider training data poisoning attacks on linear regression models. Both attack and defense methods for the linear regression task are provided with theoretical guarantees on the convergence and optimality of their attack and defense algorithms.
ANTIDOTE
Benjamin I. P. Rubinstein, Blaine Nelson, Ling Huang, Anthony D. Joseph, Shing-hon Lau, Satish Rao, Nina Taft, and J. D. Tygar. “Antidote: understanding and defending against poisoning of anomaly detectors.” Proceedings of the 9th ACM SIGCOMM Conference on Internet Measurement, 2009. [PDF]
Background of Traffic Matrix and PCA-based Defense
To uncover anomalies, many network anomography detection techniques mine the network-wide traffic matrix, which describes the traffic volume between all pairs of Points-of-Presence (PoP) in a backbone network and contains the collected traffic volume time series for each origin-destination (OD) flow.
There is a network with \(N\) links and \(F\) OD flows and measure traffic on this network over \(T\) time intervals. The relationship between link traffic and OD flow traffic is concisely captured in the routing matrix \(A\). This matrix is an \(N \times F\) matrix such that \(A_{ij} = 1\) if OD flow \(j\) passes over link \(i\), and is 0 otherwise. If \(X\) is the \(T \times F\) traffic matrix (TM) containing the time-series of all OD flows, and if \(Y\) is the \(T \times N\) link TM containing the time-series of all links, then \(Y = XA\). We denote the \(t\)th row of \(Y\) as \(y(t) = Yt\), which is the vector of \(N\) link traffic measurements at time \(t\), and the original traffic along a source link, \(S\) by \(yS(t)\).
Besides, the PCA defense method is inferring this normal traffic subspace using PCA, which finds the principal traffic components, makes it easier to identify volume anomalies in the remaining abnormal subspace.
This paper’s topic is to poisoning Principal Component Analysis anomaly detectors by poisoning the training data the detector uses (observed normal network activity), like adding additional traffic and noise to regular network traffic, to achieve a higher false negative rate.
Poisoning Strategies
Threat Model
The adversary’s goal is to launch a Denial of Service (DoS) attack on some victim and to have the attack traffic successfully cross an ISP’s network without being detected. Before launching a DoS attack, the attacker poisons the detector for a period of time, by injecting additional traffic, chaff, along the OD flow that he eventually intends to attack. For a poisoning strategy, the attacker needs to decide how much chaff to add, and when to do so. These choices are guided by the amount of information available to the attacker. The weakest attacker is one that knows nothing about the traffic at the ingress PoP, and adds chaff randomly. An intermediate case is when the attacker is partially informed. Here the attacker knows the current volume of traffic on the ingress link(s) that he intends to inject chaff on, which is locally-informed attack. An attack can also be globally-informed when the attacker’s global view over the network enables him to know the traffic levels on all network links. Moreover, we assume this attacker has knowledge of future traffic link levels.
Uninformed Chaff Selection
At each time t, the adversary decides whether or not to inject chaff according to a Bernoulli random variable. If he decides to inject chaff, the amount of chaff added is of size θ, for example, ct = θ.
Locally-Informed Chaff Selection
The attacker knows the volume of traffic in the ingress link he controls, Ys(t). Hence, this scheme elects to only add chaff when the existing traffic is already reasonably large. In particular, we add chaff when the traffic volume on the link exceeds a parameter α (we typically use the mean). The amount of chaff added is ct = (max {0, yS(t) − α}})θ.
Globally-Informed
The attacker is an omnipotent adversary with knowledge of past, present, and future network traffic. The attacker selects a link to poison and amount of chaff to add by solving an optimization problem. The optimization problem is as follows:
In this optimization problem, as we introduced before, Y contains time series of all links; A is the rounting matrix; C is the amount of chaff; $$ \widetilde{y_t} $$ is the link volume in future time t; μ is mean traffic vector; θ is a constant constraining total chaff.
ANTIDOTE: A ROBUST DEFENSE
This paper propose an approach searches for directions that maximize a robust scale estimate of the data projection to make PCA robust. Together with a new robust Laplace threshold, they form a new network-wide traffic anomaly detection method, Antidote. To mitigate the effect of poisoning attacks, this paper needs a learning algorithm that is stable in spite of data contamination. That learning algorithm can be robust PCA since robust is the formal term used to qualify this notion of stability.
The aim of a robust PCA is to construct a low dimensional subspace that captures most of the data’s dispersion and is stable under data contamination. The robust PCA algorithms we considered search for a unit direction v whose projections maximize some univariate dispersion measure S(·); that is
The standard deviation is the dispersion measure used by PCA.
Unlike the eigenvector solutions that arise in PCA, there is generally no efficiently computable solution for robust dispersion measures and so these must be approximated. So this paper proposed PCA-GRID, which is a successful method for approximating robust PCA subspaces.
To better understand the efficacy of a robust PCA algorithm, this paper demonstrates the effect our poisoning techniques have on the PCA algorithm and contrast them with the effect on the PCA-GRID algorithm.
PCA-GRID
Here the data has been projected into the 2D space spanned by the 1st principal component and the direction of the attack flow. The effect on the 1st principal components of PCA and PCA-GRID is shown under a globally informed attack (represented by points).
Robust Laplace Threshold
Instead of the normal distribution assumed by the Q-statistic, this paper use the quantiles of a Laplace distribution specified by a location parameter c and a scale parameter b. Critically, though, instead of using the mean and standard deviation, this paper robustly fit the distribution’s parameters. Then, they estimate c and b from the residuals ya(t)2 using robust consistent estimates of location (median) and scale (MAD).
where \(P^{−1}(q)\) is the qth quantile of the standard Laplace distribution. The Laplace quantile function has the form ((P^{−1}_{c,b}(q) = c+b·k(q)\) for some k(q).
Methodology
They first collected data over a 6 month period, consisting of measurements across network flows. They wanted to evaluate the how good ANTIDOTE is in the face of poisoning and DoS attacks. They used two weeks of data for this, the first for testing and second for training. The poisoning occurs during the training phase, and the attack occurs during the test week. They also had a second method where training and poisoning occurred over multiple weeks, called the Boiling Frog method. They determined success by the false negative rate (FNR), or the number of successful evasions to attacks.
To compute FNRs, they generated anomalies by the Lakhina et al. method and injected into collected data. Data is binned in 5 minute windows, and they make a decision at the end of each 5 minute window whether or not there was an attack. In terms of FPRs, they generate negative examples, fit the data to a model. Selected points in the data that differ from the model by a small amount are “benign.” If the detectors raise an alarm for these points, we have a false positive. They also carried out the Boiling Frog method which has a complicated mathematical procedure and can be understood further by reading the paper.
Effectiveness of Poisoning
During the testing phase, a DoS attack was launched during the 5 minute windows of the single training experiment. The graph below indicates evasion is smallest with the uninformed strategy, intermediate for the locally-informed strategy, and largest for the globally-informed strategy. This makes sense since naturally the globally-informed attacker would know more than the others.
For the multi-training poisoning (boiling frog), the schedules were varied with increasing growth rates from week to week. The evasion graph is shown below. The three slower schedules have a small rejection rate. The 15% schedule has a higher rejection rate, but after a month of injected poison data, the rates drop off.
How well does ANTIDOTE perform in the face of attacks?
We can see that the evasion success of the attack is dramatically reduced with ANTIDOTE in the figure below if we compare it to the evasion graph for single training poisoning in the previous section. The evasion success is cut in half. The most effective poisoning scheme on PCA was globally informed, but with their solution was the most ineffective scheme.
With the boiling frog strategy, we can see the results in the graph below. For the stealthiest poisoning (1.01 and 1.02), antidote is most effective in reducing evasion success. Also, under PCA the evasion increased with time. However, with ANTIDOTE, evasion success starts to drop off after some time.
References
[1] Matthew Jagielski, Alina Oprea, Battista Biggio, Chang Liu, Cristina Nita-Rotaru and Bo Li. Manipulating Machine Learning: Poisoning Attacks and Countermeasures for Regression Learning. April 2018.
[2] Xiao, Huang, et al. “Is feature selection secure against training data poisoning?". International Conference on Machine Learning. 2015.
[3] Fischler, Martin A., and Robert C. Bolles. “Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography.” Readings in computer vision. 1987. 726-740.
[4] Huber, Peter J. “Robust estimation of a location parameter.” The annals of mathematical statistics (1964): 73-101.
[5] Chen, Yudong, Constantine Caramanis, and Shie Mannor. “Robust sparse regression under adversarial corruption.” International Conference on Machine Learning. 2013.
[6] Nelson, Blaine, et al. “Exploiting Machine Learning to Subvert Your Spam Filter.” LEET 8 (2008): 1-9.
[7] Ali Shafahi, W. Ronny Huang, Mahyar Najibi, Octavian Suciu, Christoph Studer, Tudor Dumitras, and Tom Goldstein. “Poison Frogs! Targeted Clean-Label Poisoning Attacks on Neural Networks.” April 2018.
[8] Szegedy, Christian et. al. “Rethinking the inception architecture for computer vision.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2016): 2818–2826.
[9] Rubinstein, Benjamin IP, et al. “Antidote: understanding and defending against poisoning of anomaly detectors.” Proceedings of the 9th ACM SIGCOMM conference on Internet measurement. ACM, 2009.
Class 10: Formal Verification Methods
Motivation
Similar to what we saw in Class 6, we would like to have formal bounds on how robust a machine learning model under attack. The following two papers aim at achieving this robustness by means of proving properties about the underlying neural networks. This strategy aims to end the arms race of attacks and defenses commonly seen in literature, and to provide formal guarantees of defenses with respect to any type of adversary.
Differential Privacy and Adversarial Robustness
Mathias Lecuyer, Vaggelis Atlidakis, Roxana Geambasu, Daniel Hsu, Suman Jana. On the Connection between Differential Privacy and Adversarial Robustness in Machine Learning. February 2018. arXiv e-print [PDF]
In the privacy domain, we are able to provide formal guarantees of the privacy of records by introducing the property of differential privacy. Where for two data sets that differ in one record, the difference of the output predictions on each one is less than some bounded amount.
In this paper, the authors extend this property to apply to adversarial examples by relating changes in a data set to changes in an input. Where for two inputs that differ in some perturbation, the difference of the output predictions on each one is less than some bounded amount.
More formally, $$ P(A(x) = i) \le e^{\epsilon} P(A(x’) = i) + \delta $$ Where, \( x’ \) is some perturbed version of \( x \). \( A \) is the algorithm in question, and \( P(A(x) = i) \) is the probability that A assigns to \( x \) taking on value \( i \).
The authors apply this property to images and call it PixelDP. They go on to prove that if a model satisfies PixelDP with respect to the 0-norm metric for a set of inputs, then it is robust to 0-norm attacks on those inputs. (0-norm here indicating how many pixels were changed).
They accomplish this by also establishing an upper bound on the second highest class assignment for the perturbation, \( \max_{j \ne i} p_j(x’) \), using the same principle of robustness as defined above:
$$ P(A(x’) = j) \le e^{\epsilon}P(A(x) = j) + \delta $$
From these two bounds, they arrive at the core proposition that an algorithm satisfies PixelDP robustness to 0-norm attacks if the following holds:
$$ p_{i}(x) > e^{2 \epsilon} \max_{j: j \ne i} p_{j}(x)+ (1+e^{\epsilon}) \delta $$
(sorry, can’t get this to typeset with mathjax).
With this proposition the authors devise a method for attaining this property, primarily by adding and accounting for noise during training and testing.
Noise Layer
The authors’ basic approach is to add a noise layer to the neural network. They first establish that the noise added should be proportional to the sensitivity of the layer, which is more difficult to compute for deeper layers. They recommend placing the noise in the first few layers of the network as it is easiest to bound the sensitivity, and acknowledge that trade-offs of accuracy and robustness play a role in the decision process.
The noise layer itself simply uses Laplacian and Gaussian mechanisms to add noise, and the network is trained with the noise layer to allow decent accuracy.
Testing Strategy
To account for the noise during testing, the authors run the input through the network multiple times. The label is the highest predicted score is chosen and these results are counted and aggregated. This allows the variance of each label to also be computed.
The idea of making multiple queries may seem contradictory to the idea of privacy, where each query takes away from a privacy budget. However, here we are not concerned with privacy leakage here, only with bounding the output of the function.
Robustness
Finally, to have a measure of robustness, the authors propose a way deriving a bound for the maximum perturbation allowed. This is accomplished by finding the maximum \( L \) such that the proposition defined above still holds. The resulting \(L\)max can be compared against some threshold \( T \) such that if \( L_{max} \ge T \) then the model is robust against that input. That is to say, that perturbation to the given image would not be sufficient to change its label.
This metric is, of course, dependent on a given test set, but it allows the claim that a certain portion of the test set is “safe”, meaning the prediction is robust for that test set. If the test set is representative of the input domain examples that matter, this can give us some confidence (but no guarantee) that the model is robust for other inputs also.
Evaluation
To evaluate their approach, the authors used three accuracy metrics.
- Conventional accuracy: the proportion of correct predictions
- Robust accuracy: the proportion of correct and robust predictions
- Robust precision: the proportion of correct predictions relative to the number of robust predictions.
They first tested accuracy on benign samples with different noise levels, \( L \) and different thresholds for robustness \( T \).
They found that, with higher \( T \), robust accuracy decreases but robust precision increases, and that the threshold should be tuned based on the amount of noise.
They then tested the accuracy on malicious samples, comparing to the Madry defense [3]
This shows that for a 2-norm attack, their defense is comparable to the Madry defense, but for an inf-norm attack, the Madry defense is better. These results make sense because the Madry defense was built around \( L\)\(\infty\) attacks, while PixelDP is for \( L\)0 and \( L\)2 attacks. This begs the question of if we can have a differential privacy based defense in the \(L_{\infty} \) space, but at the moment there is no clear mapping between the two.
Piecewise Linear Neural Network Verification
Rudy Bunel, Ilker Turkaslan, Philip H.S. Torr, Pushmeet Kohli, M. Pawan Kumar. Piecewise Linear Neural Network verification: A comparative study. arXiv e-print November 2017. [PDF]
In this paper, the authors look at providing guarantees for piecewise linear neural networks for the purposes of verification. They show how to approach this through several approaches. For all of these approaches, the problem is defined the same general way. We are given a network that implements a function \( y = f(x) \) and some bounded input domain \( C \) in order to prove some property \( P \) about the network. This can be formulated as shown below: $$ x \in C, y = f(x) \implies P(y) $$
In this problem definition, we see that we are only considering piecewise-linear neural networks (PL-NNs). This is justified by the observation that PL-NNs represent the majority of networks used in practice. In addition, the properties mentioned in the problem statement are defined to be Boolean formulas over linear inequalities.
Verification Methods
The authors then go on to discuss a couple different verification methods, which all leverage the piecewise linear structure of PL-NN. All of these methods that are compared follow the same general principle: discover a counterexample to make the given property false. If this counterexample problem is unsatisfiable, then we have shown that no counterexample exists and hence the property must be true.
Mixed Integer Programing Encoding
In the general problem we are taking a look at, we have an issue with non-linearities as we must deal with a max function on the output of our network. In this method, the authors bypass this by replacing these nonlinear max functions with a set of inequalities. These can then be passed off to the solver to see if we can achieve some counterexample.
Reluplex
This method essentially assigns values to all the variables, even if some of the constraints are violated. It then goes through and tries to fix the violated constraints at each step. Reluplex is covered more extensively in our previous blog post.
Planet
This method operates by attempting to find an assignment to the phase of the non-linearities. Similar to Reluplex, it assigns values to the variables and then at each step verifies the feasibility of the assignment. Unlike Reluplex, this also has the advantage of being easily extended to networks containing MaxPooling units. In order to detect incoherent assignments, the author also employs a global linear approximation to the neural network. This is done by approximating the nonlinear constraints as a set of linear constraints that represent the convex hull of the nonlinearities.
Branch and Bound Optimization for Verification
This method looks at transforming this whole satisfiability problem into an optimization problem. To approach this, we look at adding extra neurons to the end of the network such that we can take a look at the global minimum and use that information to determine whether the original problem was satisfiable. Essentially, we are formulating any Boolean formula over linear inequalities on the output of the network as a sequence of additional layers, and thus reducing the verification problem to a global minimization problem.
Optimization algorithms, such as stochastic gradient descent, are not appropriate for this minimization problem as they do not provide the guarantee of a global minimum. The authors thus propose a branch and bound algorithm. This algorithm essentially is a breadth-first search algorithm. The algorithm computes the upper and lower bounds of the minimum of the output. The best upper-bound found so far will serve as a candidate for the global minimum. The iterative splitting process of the BFS type search will allow us to get a tighter and tighter lower bound.
Evaluation
For the evaluation, they consider a couple of data sets: Airborne Collision Avoidance System, Collision Detection, and Twin Stream. For each of these, they attempt to solve the satisfiability problem with a timeout of two hours. They define their success rate to be the proportion of properties successfully solved. A problem determined as SAT means that the property was false and that a counterexample exists and hence, UNSAT means that the property is true. Another metric used is labeled “Number of Wins.” This counts the number of times a solver was the fastest to solve a property. The results for these data sets are shown below:
Overall, we can see that the proposed branch and bound method is able to compete with other verification methods present in literature and so this proposes a new strategy for formal verification techniques.
Suman’s Talk
For the last section of class, Suman Jana from Columbia University gave us a talk on his ongoing research. He also discussed some of the core motivations for why it is important and difficult to study this area. Citing the differences between testing and verifying regular programs, which can have formal specifications and SMT solvers. In machine learning, the idea is to learn the specification, and they are fundamentally much more opaque.
— Team Bus:
Anant Kharkar,
Atallah Hezbor,
Bhuvanesh Murali,
Mainuddin Jonas,
Weilin Xu
References
[1] M. Lecuyer, V. Atlidakis, R. Geambasu, D. Hsu, S. Jana. “On the Connection between Differential Privacy and Adversarial Robustness in Machine Learning” arXiv preprint arXiv:1802.03471, February 2018.
[2] R. Bunel, I. Turkaslan, P-H.S. Torr, P. Kohli, M.-P, Kuymar. “Piecewise Linear Neural Network verification: A comparative study” arXiv preprint arXiv:1711.00455, November 2017.
[3] A. Madry, A. Makelov, L. Schmidt, D. Tsipras, A. Vladu. “Towards Deep Learning Models Resistant to Adversarial Attacks” arXiv preprint arXiv:1706.06083, June 2017.
Class 9: Adversarial Malware Detection
Evolution of the Malware Arms Race
Babak Bashari Rad, Maslin Masrom, and Suhaimi Ibrahim. Evolution of Computer Virus Concealment and Anti-Virus Techniques: A Short Survey. University Technology Malaysia. 6 April 2011. [PDF]
Since the first appearances of early malware, advances in both combating and creating viruses have analogously mirrored the general patterns of the medical battle against evolving biological virus outbreaks — as anti-virus software continually develops innovative techniques for detecting existing viruses, virus writers seek out new methods to cheat those detection systems. To understand the present state of the field and the role of machine learning in combating malware, let’s look at a brief history of how both the attacks and defenses have evolved in the malware domain.
Encrypted Viruses
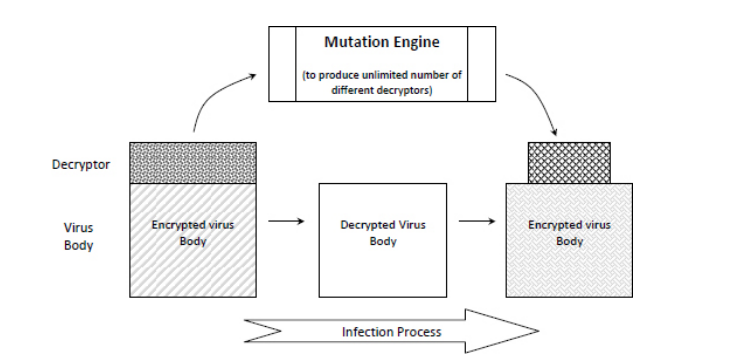
At its most basic, a virus is simply a program that is designed to alter the way a computer operates and spread from one computer to another. However, to be truly effective, a virus must also conceal itself so as to replicate and infect another computer. Thus, the most primitive approach to covering the operation of the virus code, first appearing in 1988, uses encryption to change the virus body binary codes with encryption algorithms in order to make it more difficult to analyze and detect.
Encrypted viruses are typically made up of two parts: the encrypted body of the virus itself, and a small (unencrypted) segment of decryption code. When the infected program runs, the decryption loop executes, which first decrypts the encrypted virus code, and then moves the program control to the body of the virus code:
Encryption has utility for a virus writer in several ways; most importantly, it disguises suspicious code in order to avoid detection by static code analysis, which automatically analyzes code and generates a warning were the code simply in unencrypted plaintext. Additionally, encryption of a virus also prevents tampering - since new viruses could accidentally produced with minor changes in the original virus code, encryption ensures that an expert is required to dismantle the virus, or else run the risk of producing further harm by messing with it. Finally, an encrypted virus cannot be detected by simple string matching prior to decryption, because only the decryptor loop is identical in all variants of the virus. Thus, in an anti-virus inspection, which attempts to match the signature for an encrypted virus, the signature string is constrained and must be selected precisely.
Morphic Viruses
The constant decryptor loops turned out to be the downfall of static encrypted viruses, however; since the decryptor loop code segment remained constant in new infected files, anti-virus software had no trouble obtaining a signature string with which to seek matches in code during an inspection. To overcome this vulnerability, virus writers employed techniques to mutate the decryptor body, giving rise to a new type of concealment viruses: oligomorphic viruses.
Rather than passing on the same exact decryptor loop code for each instance of the virus, oligomorphic viruses are willing to substitute the decryptor code in new offspring of the virus when reproducing themselves. This idea is most easily implemented by providing a set of different decryptor loops rather than one, which make the detection process more difficult for signature-based scanning engines.
In fact, the most common approach in anti-virus tools is signature scanning, which uses small strings, “signatures” (the results of manual analysis of viral codes) to identify viruses and malware. The signature is meant to discover viruses in the cases of a match, thus, it is vital to ensure that any given virus signature only maps to a specific virus, rather than mapping to say, other viruses, or worse, benign programs, in order to avoid flagging non-virus code.
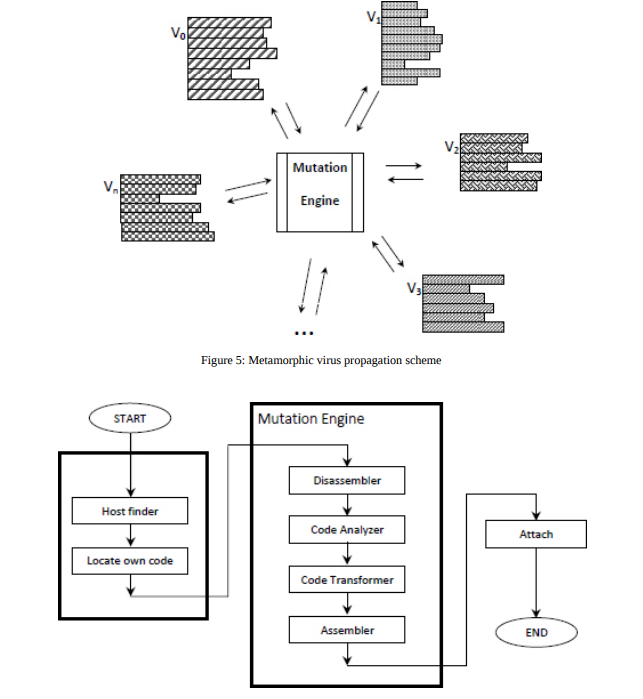
To cheat signature scanning, polymorphic viruses actually take oligomorphic viruses one step further, exploiting mutation algorithms to create a potentially infinite number of variations of decryptors in the next generation - when the virus replicates to infect a new host, it mutates its own decryptor loop to create a new permutation to pass on to the next generation. Thus, there is no consistent signature pattern from host to host that could be detected by signature scanning.
Despite these clever evasion techniques, in all the previous viruses described, once the virus body is decrypted, it is easily detected by signature scanning in its plaintext form. Polymorphic viruses, however, also dubbed “body-polymorphics”, do not even require encryption to avoid detection - instead, they mutate their entire body, rather than just their decryption loop, using the same decryptor loop-generation techniques used by polymorphic viruses to produce new instances of the virus.
Machine Learning in Malware
Konrad Rieck, Thorsten Holz, Carsten Willems, Patrick Düssel, Pavel Laskov. Learning and Classification of Malware Behavior. 15th USENIX Security Symposium. 23 April 2008. [PDF]
When an unknown malware instance is discovered, there are two important questions to be asked:
-
Does the new malware instance belong to a known malware family, or does it constitute a novel malware strain?
-
What behavioral features are discriminative for distinguishing instances of a given malware family from others?
To approach automating the discovery of the answers to this question, Rieck et al. train a classifier on honeypots and spam-traps to map unknown viruses to malware families, or to a new classification altogether, and to uncover properties that characterize families of viruses.
First, the behavior of each binary is monitored in sandbox envrionment, and behavior-based analysis reports summarizing operations. Then, the learning algorithm embeds the generated analysis reports in a high-dimensional vector space and learns a discriminative model for each malware family - that is, creates a model to predict whether this instance belongs to a known family or not, which is then aggregated against other similar models to produce a final decision. This process answers the first question.
Further, to understand and evaluate the importance of specific features for malware behavior classification, sort the weights of behavioral patterns in the learning model and consider the most prominent patterns to obtain characteristic features of each malware family.
PDF Malware Classifiers
Charles Smutz and Angelos Stavrou. Malicious PDF Detection using Metadata and Structural Features. ACSAC 2012. [PDF]
Portable Document Format (PDF)
The Portable Document Format (PDF) file structure consists of four parts: header, body, cross-reference table (CRT), and trailer. The following figures show an example PDF file, the raw content of an example PDF file, and the corresponding structural tree of the PDF file, respectively.
PDF documents have become a prevalent target of either massive or one-on-one attacks due to their wide use and diverse functionality. Popular PDF malware detectors include SL2013, Hidost, PDFRate and its variations. Among them, SL2013 and Hidost are structure-based PDF classifiers while PDFRate is content-based.
PDFRate
PDFRate, a real learning-based system introduced by George Mason University scholars Smutz and Stavrou, uses metadata and structural features to classify PDF files as benign or malicious based on the Random Forest algorithm. The feature space of PDFRate contains 202 integer, floating point and Boolean features selected from PDF metadata and file contents. Two strategies were employed during the feature selection phase, including avoiding reliance on specific byte sequence and not targeting specific known vulnerabilities. Moreover, the significant interdependence nature of the features makes the adversary’s life difficult when they attempt to control feature values. Datasets Contagio, Operational, and Community have ever been adopted in the training and evaluation of PDFRate. With respect to the classification algorithm, the number of trees is 1000 and each tree carries 43 features.
The following are the most important features for classification out of a total of 202 features: count_font count_javascript count_js count_stream_diff pos_box_max image_totalpx producer_len
Adversarial Analysis
Using PDFRate, the classification rates achieve well above 99% true positive rates while maintaining 0.2% or less false positive rates for different datasets, classification parameters and experimental conditions.
Mimicry attack, in which malicious documents are artificially modified to make some of the features similar to benign ones while retaining the malicious part, is one conceivable evasion technique. The key part the attacker want to make use of in order to spoof the defender is to mimicking the most important features for classification.
In the mimicry attack effectiveness test where the previously extracted features are purposefully modified, the six most important features were selected for evasion testing. As shown in the table below, the conclusion is that the classification error can increase to a great extent.
When the top features ranked by random forests are removed, the table below demonstrates the increase in classification error but the effect is surprisingly low. The reason is that there are many other important features retained.
The table below shows the testing results of the effectiveness of perturbation. The goal of using perturbation, i.e. increasing the feature variance by modifying the features of a malicious subset in the training set, is to reduce the importance of these features without fully negating them in order to counter evasion.
Since this approach is behavioral-based rather than signature-based, it can both identify and capture the most important behaviors of similar malware, allowing for detection that does not rely on the exact signature-matching, but rather on automated learning of behavioral patterns. This provides evidence to the claim that machine learning could provide innovative avenues into the malware field.
The findings of this study that the ensemble classifier is able to offer robust detection to counter mimicry attack even when the top features are exploited by the attacks is exciting. The classifier proves to be robust and resilient against mimicry attacks. Future directions to explore include applying the detection and classification techniques to other document types, studying the suitability of group malicious documents using the features for classification, combining other features, and performance comparative study with other techniques.
Hidost: A Static Machine-Learning-Based Detector of Malicious Files
Nedim Šrndić and Pavel Laskov. Hidost: a static machine-learning-based detector of malicious files. EURASIP Journal on Information Security, 2016. [PDF] (earlier version in NDSS 2013: [PDF])
There has been a substantial amount of work on the detection of no-executable malware which includes static, dynamic and combined methods. Although static methods perform in orders of magnitude faster, their applicability has been limited to only specific file formats. Hidost introduces the static machine-learning-based malware detection system to operate multiple file formats like pdf or swf having hierarchical document structure.
Hierarchically structured file formats
File formats are developed as a mean to store the physical representation of certain information but all of them do not have logical structure. For example, some formats like text files do not have any logical structure but others e.g.; HTML files represents a logical relationships between html elements. The following figure shows the hierarchical structure of the swf file. The pdf file structure has been discussed in the above section.
Distinguishing benign from malicious files
In a pdf structural tree, a path is defined as a sequence of edges starting in the Catalog dictionary and ending with an object of primitive type. For example, as we see in the above figure of pdf structural tree, there s a path from the root path from the root, i.e., leftmost, node through the edges named /Pages and /Count to the terminal node with the value 2. This definition of a path in the PDF document structure, which is denoted as PDF structural path, plays a central role in Hidost approach. Paths are printed as a sequence of all edge labels encountered during path traversal starting from the root node and ending in the leaf node. The path from our earlier example would be printed as /Pages/Count.
Following is a list of example structural paths of real world benign files: /Metadata /Type /Pages/Kids /OpenAction/Contents /StructTreeRoot/RoleMap /Pages/Kids/Contents/Length /OpenAction/D/Resources/ProcSet /OpenAction/D /Pages/Count /PageLayout
Presence of these structural paths in a file indicates that it is benign. Alternatively, the absence of these paths is indicative to the fact that the file may be malicious. In addition, malicious files are not likely to contain metadata in order to minimize file size, they do not jump to a page in the document when it is opened and are not well-formed so they are missing paths such as /Type and /Pages/Count. The following is a list of structural paths from real-world malicious PDF files: /AcroForm/XFA /Names/JavaScript /Names/EmbeddedFiles /Names/JavaScript/Names /Pages/Kids/Type /StructTreeRoot /OpenAction/Type /OpenAction/S /OpenAction/JS /OpenAction
System Design
The system design of Hidost consists of six stages: structure extraction, structural path consolidation, feature selection, vectorization, learning, and classification as it is illustrated in the following figure.
File structure extraction
In this stage, files are transformed into more abstract representation (logical structure) i.e.; into a structural multimap. Multimap is basically a map with associations between every structural path to the set of all leaves that lie on a given path. The concept is similar to map but you have multiple leafs as we see in path mediabox in the following figure.
Structural path consolidation
There may be cases in which semantically equivalent, but syntactically different structures can avoid detection. In Hidost, heuristic technique to consolidate structural paths to reduce polymorphic paths. For example, /Pages/Kids/Resources and /Pages/Kids/Kids/Resources can be reduced to /Pages/Resources.
Feature Selection
Feature Selection is used to limit the rare features once again similar to many Machine Learning techniques.
Vectorization
In the vectorization stage, structural multimaps are first replaced by structural maps—ordinary map data structures that map a structural path to a corresponding single numeric value. To this end, every set of values corresponding to one structural path in the multimap is reduced to its median.
Learning and Classification
The authors have used Random Forest implementation at this stage. But, it can be any classifier as per reader’s choice.
Experimental evaluation
The authors run their experiment on two datasets, one for PDF and one for SWF file formats. Both of the datasets were collected from VirusTotal. A file is considered as malicious if it is labeled as malicious by at least five engines. Alternatively, a file is labeled benign by all antivirus engines. Following figure shows that HiDost performs better that the antivirus engines in the VirusTotal. It should be mentioned that VirusTotal may not contain the most efficient antivirus developed by the proprietor company.
Machine Learning on Malware is Hard
While machine learning algorithms have been successfully applied in various vision and natural language related tasks, they have not been fully successful in malware detection. The reasons are mainly three-fold:
High Cost of Error
In the case of malware detection, when measuring the performance of a classifier, both false positive rate and false negative rate are important factors. While the false positive rate means a benign software is classified as a malware, in the false negative case a malware is classified as benign. Both the events are undesirable for malware detection. Since, false positive requires excessive spending of a human analyst’s time which could be expensive and time consuming. On the other hand, false negative means a malware is left undetected, which can have serious security consequences. A typical machine learning model trained for the malware detection task tends to have non-zero false positive rates and false negative rates.
The above figure shows the example performance of a typical malware classifier (B) which has non-zero false positive rate, whereas an ideal classifier (A) would have zero false positive rate.
Semantic Gap
There is a disconnect between the prediction result of a machine learning model and the action to be taken based on the result. For instance, if a model predicts a malware with 65% confidence, what action should be taken? Should the target software be removed without intimation to the end user? Should the user be alerted for a manual inspection? In such a scenario, it is hard to interpret the results and take a meaningful action.
Difficulty with Evaluation
One of the major difficulty in the evaluation of malware detection tool is the availability of datasets. Most of the public datasets like Contagio or Drebin are small or outdated, whereas the malwares keep updating aggressively. It is difficult to create new rich malware datasets due to data privacy concerns and the labelling of malwares in the wild. This poses problem for training and evaluating the machine learning models.
Another difficulty is the evasiveness of the malwares. Malwares have become dynamic enough to evade the malware classifiers. Given a white-box access to the classifier, malware can perform adversarial training like gradient-based method to evade detection. Even with black-box access, the malware can perform mimicry attack by appending features of benign samples. Figure below shows an example of mimicry attack. The file on the right is a benign file and the file on the left is a malicious file. By appending some features from benign file to malicious file, the classifier can be fooled into accepting the malicious file as benign.
However, this may or may not break the malware’s functionality and hence it is hard to generate useful samples. One variant is to use reverse-mimicry attack by embedding malicious features into benign file to generate malicious samples as shown in the figure below.
Recent literature has also shown evasion by genetic mutation and hill climbing method, where the malware can dynamically adapt to evade detection.
In genetic mutation attack, adversarial malware samples are generated by repeated operations on the malware sample until it is accepted as a benign sample by the classifier. The operations are addition, deletion or replacement of benign file features to the malicious file. The process only requires a binary output by the classifier whether the input was classified as malicious or not.
In hill climbing method, malicious file is taken as input and all possible recursive variants are tried until the malicious file is accepted as benign by the classifier while the malicious functionality is retained by the file. In figure below, the state e is the end state where the process has found the required adversarial sample, and the process terminates.
Both the genetic mutation and hill climbing methods are shown to fool PDF Rate and Hidost malware classifiers.
State of the Art
Liang Tong, Bo Li, Chen Hajaj, Chaowei Xiao, Yevgeniy Vorobeychik, “Hardening Classifiers against Evasion: the Good, the Bad, and the Ugly.” arXiv:1708.08327. August 2017. [PDF] [4]
Anti-malware defenders today attempt to passively analyze files of a specific type across the web and flag potential malware. These models are often trained offline. The counterparts to these software work much more actively to produce mis-classified malware. These attackers work against black box or often black-world (no response) classifiers.
Behavior Preservation
Malware behavior preservation is difficult due to the nature of code; most changes risk breaking the code entirely. This means that random mutation processes need to be heavily limited to preserve the behavior of the code. Mutation processes are often either trivial or not done at all. Very few papers allow mutations and verify the process afterward, as it requires dynamic analysis in a sandbox.
For this reason, malware development turns often to genetic development algorithms for finding evasive samples. The nature of these changes is more likely to preserve the behavior of the malware whilst creating a new sample that may be more evasive.
EvadeML
Malware development in search of evasive samples is often done using genetic algorithms mostly using greedy searches. EvadeML is one such development process to create evasive PDF malwares targeting Hidost and PDFrate. The software has a 100% success rate within 20 generations and works by mutating the raw PDFs.
The below graph plots the number of evasive specimen in a population of 500 malicious seeds against the generation using the above evolutionary method. As is readily apparent, evasive malicious samples are not only easy to produce using a small number of generations, but are also numerous. This calls into question the value of the classifiers that we are using to identify malicious code.
EvadeML is also working on a project that would ideally limit the featurespace, thus enabling better targetted classifiers. This is done via a process called feature squeezing. This process is primarily important in the filter sections displayed below, as the featurespace is limited to fewer variables to be passed through a model.
For each filter, a number of new features are selected as some function of the original feature set. This works similarly to the first layer of a neural network, except that there is more human involvement, other functions can be and are used, and that once the filter function has been created, it in unchanged during the model training process. These filters can be built from rounding/cutoff functions, input smoothing, simplifying color bit depth, and other functions that a neural net is generally incapable of creating naturally. The goal of these is to complement defensive methods and work directly to limit the potential of adversarial training.
Deep Learning
There’s a slight disconnect between security researchers and pure ML researchers, particularly those that are doing research into deep learning. The deep learning architectures that are being researched for malware deterction are multi-layer perception on preselected features and convolutional networks, but there are very few recurrent models.
Detection softwares are working to identify dynamic features more specifically in malware, as any static features of the code aren’t being triggered at runtime. This shift minimizes the attackers’ ability to mutate their code while maintaining functionality. This does, however, enable ‘time-bomb’ style malware, where certain malicious features are static until a certain datetime.
Future of the Field
While progress is being made in the field, there are a number of challenges that need to be met for malware detection and evasion to evolve. Much work has been done in the area of both static analysis and the mutation of static features. However, it’s clear that static analysis isn’t good enough for today’s tasks, and that effective detectors and mutators need to embrace dynamic features.
The more challenging goal of using a learning model to algorithmically mutate dynamic features that preserve the functionality of original code is a more complex problem. While achieving effective dynamic feature mutation isn’t currently feasible with today’s research, a step in the right direction will certainly involve selecting an appropriate deep learning architecture. Perhaps recurrent neural networks, which fit sequence modeling tasks well, could be useful.
Detectors must evolve as well. Research has shown that some dynamic analysis algorithms are detectable, and that sophisticated threats can delay malicious behavior until they are no longer in a sandboxed environment. Effectively learning from sandboxed data streams and system calls will open up a new front in the arms race between detector and attacker.
Ultimately, from simple to metamorphic viruses, malware has evolved into increasingly sophisticated threats. The field of adversarial malware detection has been evolving as well, as methods are developed that are increasingly effective at detecting malicious code. As the cutting edge of malware detection moves forward, we will see new fronts open up in the contest between malicious files and the algorithms that detect them.
— Team Nematode: \
Bargav Jayaraman, Guy “Jack” Verrier, Joshua Holtzman, Max Naylor, Nan Yang, Tanmoy Sen
References
[1] Babak Bashari Rad, Maslin Masrom, and Suhaimi Ibrahim, “Evolution of Computer Virus Concealment and Anti-Virus Techniques: A Short Survey.” IJCSI International Journal of Computer Science Issues, Vol. 8, Issue 1. January 2011
[2] Babak Bashari Rad, Maslin Masrom, and Suhaimi Ibrahim, “Camouflage in Malware: from Encryption to Metamorphism.” IJCSNS International Journal of Computer Science and Network Security, VOL.12 No.8. August 2012.
[3] Konrad Rieck, Thorsten Holz, Carsten Willems, Patrick Düssel, Pavel Laskov, “Learning and Classification of Malware Behavior.” 15th USENIX Security Symposium. 23 April 2008.
[4] Liang Tong, Bo Li, Chen Hajaj, Chaowei Xiao, Yevgeniy Vorobeychik, “Hardening Classifiers against Evasion: the Good, the Bad, and the Ugly.” arXiv:1708.08327. August 2017.
[5] R. Sommer and V. Paxson, “Outside the Closed World: On Using Machine Learning for Network Intrusion Detection.” 2010 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 2010, pp. 305-316. May 2010.
[6] Weilin Xu, Yanjun Qi, and David Evans. “Automatically Evading Classifiers A Case Study on PDF Malware Classifiers.” Network and Distributed Systems Symposium 2016.
[7] Hung Dang, Yue Huang, and Ee-Chien Chang. “Evading Classifiers by Morphing in the Dark”. ACM CCS 2017.
Class 8: Testing of Deep Networks
DeepXplore: Automated Whitebox Testing of Deep Learning Systems
Kexin Pei, Yinzhi Cao, Junfeng Yang, Suman Jana. 2017. DeepXplore: Automated Whitebox Testing of Deep Learning Systems. In Proceedings of ACM Symposium on Operating Systems Principles (SOSP ’17). ACM, New York, NY, USA, 18 pages. [PDF]
As deep learning is increasingly applied to security-critical domains, having high confidence in the accuracy of a model’s predictions is vital. Just as in traditional software development, confidence in the correctness of a model’s behavior stems from rigorous testing across a wide variety of possible scenarios. However, unlike in traditional software development, the logic of deep learning systems is learned through the training process, which opens the door to many possible causes of unexpected behavior, like biases in the training data, overfitting, underfitting, etc. As this logic does not exist as an actual line of code, deep learning models are extremely difficult to test, and those who do are are faced with two key challenges:
- How can all (or at least most) of the model’s logic be triggered so as to discover incorrect behavior?
- How can such incorrect behavior be identified without manual inspection?
To address these challenges, the authors of this paper first introduce neuron coverage as a measure of how much of a model’s logic is activated by the test cases. To avoid manually inspecting output behavior for correctness, other DL systems designed for the same purpose are compared across the same set of test inputs, following the logic that if the models disagree than at least one model’s output must be incorrect. These two solutions are then reformulated into a joint optimization problem, which is implemented in the whitebox DL-testing framework DeepXplore.
Limitations of Current Testing
The motivation for the DeepXplore framework is the inability of current methods to thoroughly test deep neural networks. Most existing techniques to identify incorrect behavior require human effort to manually label samples with the correct output, which quickly becomes prohibitively expensive for large datasets. Additionally, the input space of these models is so large that test inputs cover only a small fraction of cases, leaving many corner cases untested. Recent work has shown that these untested cases near model decision boundaries leave DNNs vulnerable to adversarial evasion attacks, in which small perturbations to the input cause a misclassification. And even when these adversarial examples are used to retrain the model and improve accuracy, they still do not have enough model coverage to prevent future evasion attacks.
Neuron Coverage
To measure the area of the input space covered by tests, the authors define what they call “neuron coverage,” a metric analogous to code coverage in traditional software testing. As seen in the figure below, neuron coverage measures the percentage of nodes a given test input activates in the DNN, analogous to the percentage of the source code executed on code coverage metrics. This is believed to be a better measure of the robustness test inputs because the logic of a DNN is learned, not programmed, and exists primarily in the layers of nodes that compose the model, not the source code.
Cross-referencing Oracles
To eliminate the need for expensive human effort to check output correctness, multiple DL models are tested on the same inputs and their behavior compared. If different DNNs designed for the same application produce different outputs on the same input, at least one of them should be incorrect, therefore identifying potential model inaccuracies.
Method
The primary objective for the test generation process is to maximize the neuron coverage and differential behaviors observed across models. This is formulated as a joint optimization problem with domain-specific constraints (i.e., to ensure that a test case discovered is still a valid input), which is then solved using a gradient ascent algorithm.
Experimental Set-up
The DeepXplore framework was used to test three DNNs for each of five well-known public datasets that span multiple domains: MNIST, ImageNet, Driving, Contagio/Virustotal, and Drebin. Because these datasets include images, video frames, PDF malware, and Android malware, different domain-specific constraints were incorporated into DeepXplore for each dataset (e.g. pixel values for images need to remain between 0 and 255, PDF malware should still be a valid PDF file, etc.). The details of the chosen DNNs and datasets can be seen in the table below.
For each dataset, 2,000 random samples were selected as seed inputs, which were then manipulated to search for erroneous behaviors in the test DNNs. For example, in the image datasets, the lighting conditions were modified to find inputs on which the DNNs disagreed. This is shown in the photos below from the Driving dataset for self-driving cars.
Deep k-Nearest Neighbors: Towards Confident, Interpretable and Robust Deep Learning
Nicolas Papernot, Patrick McDaniel. 2018. Deep k-Nearest Neighbors: Towards Confident, Interpretable and Robust Deep Learning. [PDF]
k-Nearest Neighbors
Deep learning is ubiquitous. Deep neural networks achieve a good performance on challenging tasks like machine translation, diagnosing medical conditions, malware detection, and classification of images. In this research work, the authors mentioned about three well-identified criticisms directly relevant to the security. They are the lack of reliable confidence in machine learning, model interpretability and robustness. Authors introduced the Deep k-Nearest Neighbors (DkNN) classification algorithm in this research work. It enforces the conformity of the predictions made by a DNN model on the test data with respect to the model’s training data. For each layer in the neural network, the DkNN performs a nearest neighbor search to find training points for which the layer’s output is closest to the layer’s output on the test input. Then they analyze the assigned label of these neighboring points to make it sure that the intermediate layer’s computations remain conformal with the final output model’s prediction.
Consider a deep neural network (in the left of the figure), representations output by each layer (in the middle of the figure) and the nearest neighbors found at each layer in the training data (in the right of the figure). Drawings of pandas and school buses indicate training points. We can observe that confidence is high when there is homogeneity among the nearest neighbors labels. Interpretability of the outcome of each layer is provided by the nearest neighbors. Robustness stems from detecting nonconformal predictions from nearest neighbor labels found for out-of-distribution inputs across different layers.
Algorithm
The psudo-code for their k-Nearest Neighbors (DkNN) that the authors introduced in ensuring that the intermediate layer’s computations remain conformal with the respect to the final model’s prediction is given below-
Basis for Evaluation
Basis for evaluating robustness, interpretability, Confidence are discussed below-
Evaluation of Confidence/ Credibility
In their experiments, they measured high confidence on inputs. From the experiment they observed that credibility varies across both in- and out-of-distribution samples. They tailored their evaluation to demonstrate that the credibility is well calibrated. They performed their experiments on both benign and adversarial examples.
Classification Accuracy
In their experiment, they used three datasets. First, hand written recognition task of MNIST dataset, SVHN dataset and the third one is GTSRB dataset. In the following figure, we can observe the comparison of the accuracy between DNN and DkNN model on three different dataset.
Credibility on in-distribution samples
Reliability diagrams are plotted for the three different datasets (MNIST, SVHN and GTSRB) below:
On the left, they visualized the estimation of confidence output by the DNN softmax and it is calculated by the probability \(arg ~max_{j} ~f_j(x)\). On the right, they plotted the credibility of DkNN predictions. From the graph, it may appear that the softmax is better calibrated than the corresponding DkNN. Because its reliability diagrams are closer to the linear relation between accuracy and DNN confidence. But if the distribution of DkNN credibility values are considered then it surfaces that the softmax is almost always very confident on test data with a confidence above 0.8. DkNN uses the range of possible credibility values for datasets like SVHN (test set contains a larger number of inputs that are difficult to classify).
Credibility on out-of-distribution samples
Images from NotMNIST is identical to MNIST but the classes are non-overlapping. For MNIST, the first set of out-of-distribution samples contains images from the NotMNIST dataset. For SVHN, the out-of-distribution samples contains images from the CIFAR-10 dataset. Again, they have the same format but there is no overlap between SVHN and CIFAR-10. For both the MNIST and SVHN datasets, they rotated all the test inputs by an angle of 45 degree to generate a second set of out-of-distribution samples.
In the above figure, the credibility of the DkNN on the out-of-distribution samples is compared with the DNN softmax on MNIST (left) and SVHN (right). The DkNN algorithm has an average credibility of 6% and 9% to inputs from the NotMNIST and rotated MNIST test sets respectively, compared to 33% and 31% for the softmax probabilities. We find the same observation for SVHN model. Here, the DkNN assigns an average credibility of 15% and 18% to CIFAR-10 and rotated SVHN inputs, compared to 52% and 33% for the softmax probabilities.
Evaluation of the interpretability
Here, they have considered the model being bias to the skin color of a person. In a recent study, Stock and Cisse demonstrate how an image of former US president Barack Obama throwing an American football in a stadium ResNet model. They reproduce their experiment and apply the DkNN algorithm to this model. They plotted the 10 nearest neighbors from the training data. These neighbors are computed by the last hidden layer of ResNet model.
On the left side of the above figure, the test image that is processed by the DNN is the same as that of the one used by Stock and Cisse. It contains 7 black and 3 white basketball players. They are similar to the color and also located in the air. They assumed that the ball play an important role in prediction. So, they ran another experiment with the same image but now cropping the image to remove the ball. Now the model predictated it as he is playing racket. Neighbor in this training class are white players. Image share certain charateristics, such as the background is green and most of the people are wearing white dresses and holding there hands in the air. In this example, besides the skin color, the position and appearance of the ball also contributed to the model’s prediction.
Evaluation of Robustness
DkNN is a step towards correctly handling malicious inputs like adversarial inputs because:
- outputs more reliable confidence estimates on adversarial examples than the softmax.
- provides insights as to why adversarial examples affect undefended DNNs.
- robust to adaptive attacks they considered
Accuracy on Adversarial Examples
They crafted adversarial examples using three algorithms: Fast Gradient Sign Method (FGSM), Basic Iterative Method (BIM), and Carlini-Wagner 2 attack (CW).
All there test results are shown in the following table. They have also included the accuracy of both undefended DNN and DkNN. By observing the table, they made a conclusion that even though the attacks were successful in evading the undefended DNN, but when the model is integrated with DkNN, then some accuracy on adversarial examples is recovered.
They have plotted the reliability diagrams comparing the DkNN credibility on GTSRB adversarial examples with the softmax probabilities output by the DNN. For DkNN, credibility is low across all attacks. Here, the number of points in each bin is reflected by the red line. DkNN outputs a credibility below 0.5 for most of the inputs. This indicates a sharp departure from softmax probabilities, which classified most adversarial examples in the wrong class with a high confidence of above 0.9 for the FGSM and BIM attacks. They also made an observation that the BIM attack is more successful at introducing perturbations than that of the FGSM or the CW attacks.
Explanation of DNN Mispredictions
In the above figure, for both clean and adversarial examples, we can observe that the number of candidate labels decreases as we move up the neural network from its input layer all the way to its output layer. Number of candidate labels (in this case k = 75 nearest neighboring training representations) that match the final prediction made by the DNN is smaller for some attacks. For CW attack, the true label of adversarial examples that it produces is often recovered by the DkNN. Again, the lack of conformity between neighboring training representations at different layers of the model characterizes the weak support for the model’s prediction.
Comparison to LID
We discussed similarities between the DkNN approach and Local Intrinsic Dimensionality [ICLR 2018]. There are important differences between the approaches, but given the results reported in the Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples (discussed in Class 3) reported on LID, it is worth investigating how robust DkNN is to the same attacks. (Note that neither of these defenses are really obfuscating gradients, so the attack strategy reported in that paper is to just use high confidence adversarial examples.)
The Secret Sharer: Measuring Unintended Neural Network Memorization & Extracting Secrets
Nicholas Carlini, Chang Liu, Jernej Kos, Ulfar Erlingsson, Dawn Song. 2018. The Secret Sharer: Measuring Unintended Neural Network Memorization & Extracting Secrets. arXiv:1802.08232. [PDF]
This paper focuses an adversary targeting “secret” user information stored in a deep neural network. Sensitive or “secret” user information can be included in the datasets used to train deep machine learning models. For example, if a model is trained on a dataset of emails, some of which have credit card numbers, there is a high probability that the credit card number can be extracted from the model, according to this paper.
Introduction
Rapid adoption of machine learning techniques has resulted in models trained on sensitive user information or “secrets”. The “secrets” may include “person messages, location histories, or medical information.” The potential for machine learning models to memorize or store secret information could reveal sensitive user information to an adversary. Even black-box models were found to be susceptible to leaking secret user information. As more deep learning models are implemented, we need to be mindful of the models ability to store information, and to shield models from revealing secrets.
Contributions
The exposure metric defined in this paper measures the ability of a model to memorize a secret. The higher the exposure of a model, the more likely a model is memorizing secret user information. The paper uses this metric to compare the ability of different models to memorize with different hyper-parameters. An important observation was that secrets were found to be memorized early in training rather than in the period of over-fitting. The author found that this property was consistent between different models and hyper parameters. Models included in paper focus on deep learning generative text models. Convolution neural network were also tested, but perform worse generally on text-based data. Extraction of secret information from the model was tested with varying hyper-parameters and conditions.
Perplexity and Exposure
Perplexity is a measurement of how well a probability distribution predicts a sample. A model will have completely memorized the randomness of the training set if the log-perplexity of a secret is the absolute smallest.
Log-perplexity suggests memorization but does not yield general information about the extent of memorization in the model. Thus the authors define rank:
To compute the rank, you must iterate over all possible secrets. To avoid this heavy computation the authors define multiple numerical methods to compute a value related to the rank of a secret, exposure.
Secret Extraction Methods
The authors identify four methods for extracting secrets from a black-box model.
- Brute Force
- Generative Sampling
- Beam Search
- Shortest Path Search
Brute force was determined to be too computationally expensive, as the randomness space is too large. Generative sampling and beam search both fail to give the most optimal solution. The author’s used shortest path search to guarantee the lowest log-perplexity solution. Their approach was based on Dijkstra’s graph algorithm, and is explained in the paper. The figure below demonstrates the process of maximizing the log-perplexity for the purpose of finding the secret.
Characterizing Memorization of Secrets
In order to better understand model memorization the authors tested different numbers of iterations, various model architectures, multiple training strategies, changes in secret formats and context, and memorization across multiple simultaneous secrets.
Iterations
As showing in the figure below, the authors collected data relating to the exposure of the model throughout training. The exposure of the secret can clearly be seen rising until the test error starts to rise. This increase in exposure expresses the model’s memorization of the training set early in the training process.
Model architectures
The authors observed, through their exposure metric, that memorization was a shared property among recurrent and convolutional neural networks. Data relating to the different model architectures and exposure is shown in the figure below.
Training strategies
As seen in the figure below, smaller batch sizes resulted in lower levels of memorization. Although having a smaller batch size slows down distributed processing of models, it is clear that their results suggest that a smaller batch size can reduce memorization.
Secret formats and context
The table below interestingly suggests that the context of secrets significantly impacts whether an adversary can detect memorization. As there become more characters or information associated with the secret, the adversary has an easier time extracting randomness.
Memorization across multiple simultaneous secrets
The table below shows the effect of inserting multiple secrets into the dataset. As the number of insertions increase, the model becomes more likely to memorize the secrets that were inserted.
Evaluating word level models
An interesting observation was that the capacity of a large word-level model produced better results than the smaller character-level model. By applying the exposure metrics to a word-level model, the authors found that representation of numbers mattered heavily in the memorization of information. When the authors replaced replaced “1” with “one,” they saw the exposure dropped by more than half from 25 to 12 for the large word-level model. Because the word-level model was more than 80 times the size of the character-level model, the authors found it surprising that “[the large model] has sufficient capacity to memorize the training data completely, but it actually memorizes less.”
Conclusion
This paper examines the extent to which memorization has occurred in different types of algorithms and how sensitive user information can be revealed through this memorization. The metrics used in the paper can be easily transferred to existing models that have a well-defined notion of perplexity. They also demonstrate that these metrics can also be used to extract secret user information from black-box models.
— Team Panda: Christopher Geier, Faysal Hossain Shezan, Helen Simecek, Lawrence Hook, Nishant Jha
Sources
Kexin Pei, Yinzhi Cao, Junfeng Yang, Suman Jana. 2017. DeepXplore: Automated Whitebox Testing of Deep Learning Systems. In Proceedings of ACM Symposium on Operating Systems Principles (SOSP ’17). ACM, New York, NY, USA, 18 pages. https: //doi.org/10.1145/3132747.3132785 [PDF]
Nicholas Carlini, Chang Liu, Jernej Kos, Ulfar Erlingsson, Dawn Song. 2018. The Secret Sharer: Measuring Unintended Neural Network Memorization & Extracting Secrets. arXiv:1802.08232. Retrieved from https://arxiv.org/pdf/1802.08232.pdf [PDF]
Nicolas Papernot, Patrick McDaniel. 2018. Deep k-Nearest Neighbors: Towards Confident, Interpretable and Robust Deep Learning. Retrieved from [PDF]
Class 7: Biases in ML, Discriminatory Advertising
Motivation
Machine learning algorithms are playing increasingly important roles in many critical decision making tasks. However, studies reveal that machine learning models are subject to biases, some of which stem from historical biases in human world that are captured in training data. Understanding potential bias, identifying and fixing existing bias can help people design more objective and reliable decision making systems based on machine learning models.
Ad Transparency
Athanasios Andreou, Giridhari Venkatadri, Oana Goga, Krishna P. Gummadi, Patrick Loiseau, Alan Mislove. Investigating Ad Transparency Mechanisms in Social Media: A Case Study of Facebook’s Explanations. NDSS, 2018. [PDF] (All images below are taken from this paper.)
What are ad transparency mechanisms in social media?
Transparency mechanisms are solutions for many privacy complaints from users and regulators. Users have little understanding of what data the advertising platforms have about them and why they are shown particular ads. The transparency mechanisms provided by Facebook are (1) the “Why am I seeing this?” button that provides users with an explanation of why they were shown a particular ad (ad explanations), and (2) an Ad Preferences Page that provides users with a list of attributes Facebook has inferred about them and how (data explanations). Twitter offers similar transparency mechanisms, including a “Why am I seeing this?” botton that provides users with an explanation of why they were shown a particular ad (ad explanations) in Twitter.
What did this paper do?
This paper reports on an investigation and analysis of ad explanations (why users see a certain ad), and an investigation of data explanations (how data is inferred about a user), which is strongly related to the ad transparency mechanisms in Facebook. This paper first introduced how ad platform in Facebook works and then evaluate the two transparency mechanisms we introduced before with some properties.
The Ad platform in Facebook
There are three main processes in the Facebook ad platform: a) the data inference process; b) the audience selection process; c) the user-ad matching process.
(a) The data inference process is the process that allows the advertising platform to learn the users’ attributes. It has three parts: (1) the raw user data (the inputs), containing the information the advertising platform collects about a user either online or offline; (2) the data inference algorithm (the mapping function between inputs and outputs), covering the algorithm the advertising platform uses to translate input user data to targeting attributes; (3) the resulting targeting attributes (the outputs) of each user that advertisers can specify to select different groups of users.
(b) The audience selection process is the interface that allows advertisers to express who should receive their ads. Advertisers create audiences by specifying the set of targeting attributes the audience needs to satisfy. Later, to launch an ad campaign, advertisers also need to specify a bid price and an optimization criterion.
(c) The user-ad matching process takes place whenever someone is eligible to see an ad. It examines all the ad campaigns placed by different advertisers in a particular time interval, their bids, and runs an auction to determine which ads are selected.
Ad Explanations and the experiments on this transparency mechanism
As you can see in the picture, there are both attritubutes and potentional attritubutes here.
This paper used 5 different properties to evaluate the performance of Ad explanations:
- Correctness: Every attribute listed was used by the advertiser
- Personalization: The attributes listed are unique to the individual
- Completeness: If all relevant attributes are included in the explanation
- Consistency: Users with the same attributes see the same explanations
- Determinism: A user would see the same explanation for ads based on the same target attributes
The paper evaluated the ad explanations by using Chrome browser extension to record ads and explanations. The experiment had 35 users’ data across 5 months. This experiment also evaluated the data explanation. This paper made simple statistics for the explanation (see the following figure). And then, it shows the results of different properties on this experiment.
Data Explanations Experiments
The data explanations is applied in “Your interests” part as shown in the following picture.
The properties here are not the same as those used in the Ad explanation part. There are 3 new properties.
- Specificity: A data explanation is precise if it shows the precise activities that were used to infer an attribute about a user.
- Snapshot completeness: A data explanation is snapshot complete if the explanation shows all the inferred attributes about the user that Facebook makes available.
- Temporal completeness: a temporally complete explanation is one where the platform shows all inferred attributes over a specified period of time.
The results of different properties on this experiment are showed below:
Conclusion
While the Ad Preferences Page does bring some transparency to the different attributes users can be targeted with, the provided explanations are incomplete and often vague. Facebook does not provide information about data broker-provided attributes in its data explanations or in its ad explanations.
Discrimination in Online Targeted Advertising
Till Speicher, Muhammad Ali, Giridhari Venkatadri, Filipe Nunes Ribeiro, George Arvanitakis, Fabrício Benevenuto, Krishna P. Gummadi, Patrick Loiseau, Alan Mislove. Potential for Discrimination in Online Targeted Advertising. Proceedings of the 1st Conference on Fairness, Accountability and Transparency, PMLR 81:5-19, 2018. [PDF]
Recently, online targeted advertising platforms like Facebook have received intense criticism for allowing advertisers to discriminate against users belonging to protected groups.
Facebook, in particular, is facing a civil rights lawsuit for allowing advertisers to target ads using an attribute called “ethnic affinity.” Facebook has clarified that “ethnic affinity” does not represent ethnicity, but rather represents a user’s affinity for content related to different ethnic communities. Facebook has agreed to rename the attribute to “multicultural affinity” and to disallow using this attribute to target ads related to housing, employment, and financial services.
However, Facebook offers many different ways to describe a set of targeted users, so it’s not adequate to disallow targeting on certain attributes. In this paper, the authors develop a framework for quantifying ad discrimination and show the potential for discriminatory advertising using the three different targeting methods on Facebooks advertising platform: personally identifiable information (PII)-based targeting, attribute-based targeting, and look-alike audience targeting.
Quantifying Ad Discrimination
The authors identify three potential approaches to quantifying discrimination.
Based on advertiser’s intent: The authors reject this approach since it is hard to measure and it does not capture unintentionally discriminatory ads.
Based on ad targeting process: This category includes existing anti-discrimination measures, like disallowing use of sensitive attributes when defining a target population. The authors reject this approach since it breaks down when there exist several methods of targeting a population.
Based on targeted audience (outcomes): This approach takes into account only which users are targeted, not how they are targeted. The authors use this approach to quantify ad discrimination since outcome-based analyses generalize independent of targeting methods.
The authors formalize outcome-based discrimination as follows:
The authors define a metric for how discriminatory an advertiser’s targeting is, inspired by the disparate impact measure used for recruiting candidates from a pool.
Define the representation ratio measure to capture how much more likely a user is to be targeted when having the sensitive attribute than if the user did not have the attribute:
$$\text{rep_ratio}_s(\mathbf{TA}, \mathbf{RA}) = \dfrac{|\mathbf{TA} \cap \mathbf{RA}_s|/|\mathbf{RA}_s|}{|\mathbf{TA} \cap \mathbf{RA}_{\neg s}|/|\mathbf{RA}_{\neg s}|}$$
where \(\mathbf{RA}_s = {u \in \mathbf{RA} | u_s = 1 }\) is the subset of the relevant audience with the sensitive attribute and \(\mathbf{RA}_{\neg s} = {u \in \mathbf{RA} | u_s = 0}\) is the complementary subset of the relevant audience without the sensitive attribute
Define the disparity in targeting measure to capture both over- and under-representation of a sensitive attribute in a target audience:
$$\text{disparity}_s(\mathbf{TA}, \mathbf{RA}) = \max\left(\text{rep_ratio}_s(\mathbf{TA}, \mathbf{RA}), \dfrac{1}{\text{rep_ratio}_s(\mathbf{TA}, \mathbf{RA})}\right)$$
Disparity must be computed based on the relevant audience \(\mathbf{RA}\) because \(\mathbf{RA}\) may have a different distribution of the sensitive attribute than the whole database \(\mathbf{D}\). The authors assume that sensitive attributes considered have the same distributions in the relevant audience as the global population, and therefore high disparity in targeting is evidence of discrimination. Following the “80%” disparate impact rule, a reasonable disparity threshold for a group to be over- or under-represented may be \(\max(0.8, 1/0.8) = 1.25\).
The recall of an ad quantifies how many of the relevant users with the sensitive attribute the ad targets or excludes:
$$\text{recall}(\mathbf{TA}, \mathbf{RA}') = \dfrac{|\mathbf{TA} \cap \mathbf{RA}‘|}{|\mathbf{RA}‘|}$$
where \(\mathbf{RA}'\) is one of \(\mathbf{RA}_s\) or \(\mathbf{RA}_{\neg s}\) depending on whether we’re considering the inclusion or exclusion of \(\mathbf{S}\).
PII-Based Targeting
PII-based targeting on the Facebook advertising platform allows advertisers to select a target audience using unique identifiers, like phone numbers, email addresses, and combinations of name with other attributes (e.g. birthday or zip code). The authors show that public data sources, such as voter records and criminal history records, contain sufficient PII to construct a discriminatory target audience for a sensitive attribute without explicitly targeting that attribute.
The authors constructed datasets to show that they could implicitly target gender, race, and age using North Carolina voter records. Each of these attributes is listed in voting records, and the remaining fields together uniquely identify the voter (i.e., last name, first name, city, state, zip code, phone number, and country). The authors uploaded datasets targeting values of each attribute and recorded Facebook’s estimated audience size.
The Voter Records column shows the distribution of attribute values in the voter records data set. For a given attribute, the Facebook Users column shows how many of the 10,000 people in the dataset constructed for that attribute are actually targetable on Facebook (as reported by the Facebook advertising platform). The final column shows the portion of the targetable users who actually match the targeted attribute, found by restricting the target audience using Facebook’s records of the sensitive attribute. High targetable percentages values show that the voter records overlap significantly with the voter records data set. High validation percentages show that the auxiliary PII was highly accurate at describing particular users with the targeted attribute. Note that there are some low validation percentages, which the authors attribute to Facebook’s inaccurate or incomplete records of some data (for example, they do not know race, only “multicultural affinity”).
Attribute-Based Targeting
Attribute-based targeting allows advertisers to select a target audience by specifying that targeted users should have some attribute or combination of attributes. The authors group these attributes into two categories: curated attributes and free-form attributes. Curated attributes are well-defined binary attributes spanning demographics, behaviors, and interests — Facebook tracks a list of over 1,100 of these. Free-form attributes describe users inferred interest in entities such as websites and apps as well as topics such as food preferences or niche interests. The authors estimate that there are at least hundreds of thousands of free-form attributes.
The authors demonstrate that many curated attributes are correlated with sensitive attributes like race, and can therefore be used for discriminatory audience creation. The following table shows experimental results obtained by uploading sets of voter records filtered to contain only a single race and measuring Facebook’s reported size of the subaudiences for each curated attribute. The figures in parentheses are the recall and representation ratio for a population from North Carolina. The top three most inclusive and exclusive attributes per ethnicity are listed. Note the high representation ratios for the “Most inclusive” column and the low representation ratios for the “Most exclusive” column.
The authors similarly demonstrated that free-form attributes could used in a discriminatory manner. For example, targeting a vulnerable audience could be made possible by targeting the free-form attributes “Addicted,” “REHAB,” “AA,” or “Support group.” The authors also showed how Facebook’s attribute suggestions feature could be used to discover new highly-discriminatory free-form attributes. For example, starting a search with “Fox” (37% conservative audience on Facebook) and following a chain of suggestions leads to “The Sean Hannity Show” (95% conservative audience on Facebook).
Look-Alike Audience Targeting
Look-alike audience targeting allows advertisers to generate a new target audience that looks similar to an existing set of users (the fans of one of their Facebook pages or an uploaded PII data set). The authors show that this feature can be used to scale a biased audience to a much larger population. Experimental results suggest that Facebook attempts to determine the attributes that distinguish the base target audience from the general population and propagates these biases to the look-alike audience. The authors show that this bias propagation can amplify both intentionally created and unintentionally overlooked biases in source audiences.
Algorithmic Transparency via Quantitative Input Influence
Anupam Datta, Shayak Sen, Yair Zick. Algorithmic Transparency via Quantitative Input Influence: Theory and Experiments with Learning Systems. 2016 IEEE Symposium on Security and Privacy (“Oakland”). [PDF]
Machine learning systems are increasingly being used to make important societal decisions, in sectors including healthcare, education, and insurance. For instance, an ML model may help a bank decide if a client is eligible for a loan, and both parties may to know critical details about how the model works. A rejected client will likely want to know why they were rejected: would they have been accepted if their income was higher? The answer would be especially important if their reported income was lower than their actual income; more generally, the client can ensure that their input data contained no errors.
Conversely, the model’s user may want to ensure that the model does not discriminate based on sensitive inputs, such as the legally-restricted features of race and gender. Simply ignoring those features may not be sufficient to prevent discrimination; e.g., ZIP code can be used as a proxy for race. This paper proposes a method to solve these problems by making the model’s behavior more transparent: a quantitative measure of the effect of a particular feature (or set of features) on the model’s decision for an individual. The paper offers several approaches suited for various circumstances, but they all fall under the umbrella of “quantitative input inflence”, or QII.
Unary QII
The simplest quantitative measure presented is unary QII, which measures the influence of one attribute on a quantity of interest \(Q_\mathcal{A}\) for some subset of the sample space \(X\). Formally, unary QII is determined as
where the first term is the actual expected value of \(Q_\mathcal{A}\) for this subset, and the second term is the expected value if the feature \(i\) were randomized.
For example, consider the rejected bank client from above. If they restrict \(X\) to only contain their feature vector, and they set \(Q_\mathcal{A}\) to output the model’s probability of rejection, then unary QII tells how much any individual feature impacted his loan application. If the unary QII for a feature is large, changing the value of that feature would likely increase their odds of being accepted; conversely, changing the value of a feature with low unary QII would make little difference.
The paper presents a concrete example: Mr. X has been classified as a low-income individual, and he would like to know why. Since only 2.1% of people with income above $10k are classified as low-income, Mr. X suspects racial bias. In actuality, the transparency report shows that neither his race nor country of origin were significant; rather, his marital status and education were far more influential in his classification.
The sample space \(X\) can also be broadened to include an entire class of people. For instance, suppose \(X\) is restricted to include people of just one gender, and \(Q_\mathcal{A}\) is set to output the model’s probability of acceptance. Here, unary QII would reveal the influence of a feature \(i\) on men and on women. A disparity between the two measures may then indicate that the model is biased: specifically, the feature \(i\) can be identified as a proxy variable, used by the model to distinguish between men and women (even if gender is omitted as an input feature).
However, unary QII is often insufficent to explain a model’s behavior on an individual or class of individuals. This histogram shows the paper’s results for their “adult” dataset: for each individual, the feature that created the highest unary QII was found, and the unary QII value was plotted in the histogram. Most individuals could not be explained by any particular feature, and most features had little influence by themselves.
Set and Marginal QII
Thankfully, unary QII can easily be generalized to incorporate multiple features at once. Set QII is defined as
where \(S\) is a set of features (as opposed to a single feature, like \(i\) in unary QII). The paper also defines marginal QII
which measures the influence of a feature \(i\) after controlling for the features in \(S\). These two quantitative measures have different use cases, but both are more general (and thus more useful) than unary QII.
Marginal QII can measure the influence of a single feature \(i\), like unary QII, but only for a specific choice of \(S\), and the amount of influence can vary wildly depending on the choice of \(S\). To account for this, the paper defines the aggregate influence of \(i\), which measures the expected influence of \(i\) for random choices of \(S\).
Conclusion
The above variants of QII can be used to provide transparency reports, offering insight into how an ML model makes decisions about an individual. Malicious actors may seek to abuse such a system, carefully crafting their input vector to glean someone else’s private information. However, these QII measures are shown too have low sensitivity, so differential privacy can be added with small amounts of noise.
These QII measures are useful only if the input features have well-defined semantics. This is not true in domains such as image or speech recognition, yet transparency is still desirable there. The authors assert that designing transparency mechanisms in these domains is an important future goal. Nevertheless, these QII measures are remarkably effective on real datasets, both for understanding individual outcomes and for finding biases in ML models.
Language Corpus Bias
Caliskan, A., Bryson, J., & Narayanan, A. (2017). Semantics derived automatically from language corpora contain human-like biases. Science, 356(6334), 183-186. doi:10.1126/science.aal4230 [PDF] [Author’s Full Version PDF]
The focus of this paper is how machine learning can learn from the biases and stereotypes in humans. The main contributions of the authors are:
- Using word embeddings to extract associations in text
- Replicate human bias to reveal prejudice behavior in humans
- Show that cultural stereotypes propagate to widely used AI today
Uncovering Biases in ML
The authors began by replicating inoffensive biases using their original Word-Embedding Association Test (WEAT) method. Word embedding is a representation of words in vector space. WEAT is a test applied to words in AI which represents words as a 300 dimensional vector. The words are then paired by distances between the vectors. Using WEAT, they demonstrated that flowers have pleasant associations and insects have unpleasant associations. Or instruments are more pleasant than weapons. The word embeddings know the properties of flowers or weapons even though they have no experience with them!
After showing that WEAT works, they use this technique to show that machine learning absorbs stereotype biases. In a study by Bertrand and Mullainathan, 5,000 identical resumes were sent out to 1,300 job ads and varied only the names. The European American names were 50% more likely to be offered an opportunity to be interviewed. Based on this study, the authors used WEAT to test the pleasantness associations with the names from Bertrand’s work and found European American names were more pleasant than African American names.
They then turned to studying gender biases. Female names were associated with family as oppose to male names which were associated with career. They also showed woman/girl associated more with arts than math compared to men. These observations were then correlated with data in the labor force. This is show in the figure below:
The authors then applied another method of their creation called Word-Embedding Factual Association Test (WEFAT) to show that these embeddings correlate strongly with the occupations women have in the real world. They then used the GloVe method to find similarity between a pair of vectors. Similarity between vectors is related to the probability that the words co-occur with other words similar to each other. GloVe finds this by doing dimensionality reduction to amplify signal in co-occurring probabilities.
Afterwards, they did a crawl of the internet and got 840 billion words, and each word had a 300 dimension vector derived from counts of other words that occur with it in a 10 word window. WEFAT allowed them to further examine how embeddings capture empirical information. Using this, they were able to predict properties from the given vector.
Conclusion
So what does their work mean? Their results show there’s a way to reveal unknown implicit associations. They demonstrate that word embeddings encode not only stereotyped bias, but also other knowledge like that flowers are pleasant. These results also explain origins of prejudice in humans. It shows how group identity transmits through language before an institution explains why individuals make prejudiced decisions. There are implications for AI and ML because technology could be perpetuating cultural stereotypes. What if ML responsible for reviewing resumes absorbed cultural stereotypes? It’s important to keep this in mind and be cautious in the future.
Men Also Like Shopping: Reducing Bias Amplification
Jieyu Zhao, Tianlu Wang, Mark Yatskar, Vicente Ordonez, Kai-Wei Chang. Men Also Like Shopping:Reducing Gender Bias Amplification using Corpus-level Constraints. 2017 Conference on Empirical Methods in Natural Language Processing. arXiv preprint arXiv:1709.10207. July 2017.
Language is increasingly being used to identify some rich visual recognition tasks. And structured prediction models are widely applied to these tasks to take advantage of correlations between co-ocurring labels and visual inputs. However, inadvertently, there can be social biases encoded in the model training procedure, which may magnify some stereotypes and poses challenge in the fairness of (machine learning) model decision making.
Researchers found that datasets for these tasks contain significant gender bias and models trained on these biased dataset further amplifies these existing biases. An example provided in the paper is, the activity “cooking” is over 33% more likely to refer females than males in the training set, and a model trained on this dataset can further amplify the disparity of gender ratio to 68% at test time. And to tackle the problem, the author proposed to adopt corpus-level constraints for calibrating existing structured prediction models. Specifically, the author limit the gender bias of the model deviate by only a small amount from what is in the original training data.
Problem Formulation
The problem is then defined as maximizing the test time inference likelihood while also satisfying the corpus-level constraint. A bias score for an output \(o\) with respect to demographic variable \(g\)is defined as: $$b(o,g) = \frac{c(o,g)}{\sum_{g^{'}\in G}c(o,g^{'})}$$ where \(c(o,g)\) captures the number of occurrences of \(o\) and \(g\) in a corpus. And a bias might be exhibited if \(b(o,g)>1/||G||\). A mean bias amplification of a model compared to the bias on training data set (i.e., \(b^{*}(o,g)\)) is defined as:
with these terms defined, the author proposes the calibration algorithm: \(\textbf{R}educing~\textbf{B}ias~\textbf{A}mplification\) (RBA). Intuitive understanding the of calibration algorithm is to inject constraints to ensure the model predictions follow the gender distribution observed from the training data with allowbable small deviations.
Structured Output Prediction
Given a test insatnce, the inference problem at test time is defined as: $$\underset{y\in Y}{\operatorname{argmax}}f_{\theta}(y,i)$$
with \(f_{\theta} (y,i)\) is a scoring function based on model \(\theta\) learned from training data. The inference problem hence can be interpreted as finding the structured oupt \(y\) such that the scoring function is maximized. The corpus level constraint is expressed as:
With the given constraint, the problem is formulated as:
where \(i\) refers to insatnce \(i\) in test dataset.
The corpus level constraint is represented by \(A\sum_{i}y^{i}-b \leq 0\), where the matrix \(A\in R^{l \times K}\) is the coefficients of one constraint, and \(b \in R^{l}\). Note that, above formulation can be solved individually for each instance \(i\).
Lagrangian Relaxation
The final optimization problem is a mixed integer programming problem, and solving with off-the-shell solver is inefficient for large-scale dataset. Hence, the author proposed to solve the problem with Lagrangian relaxation technique. With a lagrangian multiplier introduced, we have the Lagrangian as
where \(\lambda_{j} \geq 0, \forall \in {1,…,l}\). The solution to the problem is then obtained by iteratively optimizing the problem with respect to \(y^{i}\) and \(\lambda\). Specifically, we need two steps in each optimization iteration:\
- At iteration \(t\), first get the output solution of each instance \(i\)
Experimental Setup
This problem is evvaluated on two vision recognition tasks: visual semantic role labeling (vSRL), and multi-label classification (MLC). The authors focus on the gender bias problem, where \(G = \{man, woman\}\) and focus on the agent and any occurrence in text associated with the images in MLC.
Dataset and Model
The experiment of vSRL is conducted on imSitu where activity classes are drawn from verbs and roles in FrameNet and noun categories are drawn from WordNet. The model is built on the baseline CRF released with the data, which has been shown effective compared to a non-structured prediction baseline [2]. The experiment of MLC is conducted on MS-COCO. The model is a similar model as CRF that is used for vSRL.
Result analysis
For both the vSRL and MLC tasks, their training data is biased as illustrated in Figure 2. Y-axis denotes the percentage of male agents and x-axis represents gender bias in training data. It is clear that many verbs are biased in the training set and when a model is trained on these biased training datasets, the gender bias is further amplified. Figure 2(a) denotes demonstrates the gender bias in vSRL task and figure 2(b) shows the gender bias in MLC task. Some seemingly neutral words like “microwaving” and “washing” is heavily biased towards female and other words like “driving” is beavily biased towards male.
Calibration results are then summarized in the table below, which utilizes RBA method. The experimental results show that, with this calibrated method, we are able to significantly reduce the gender bias.
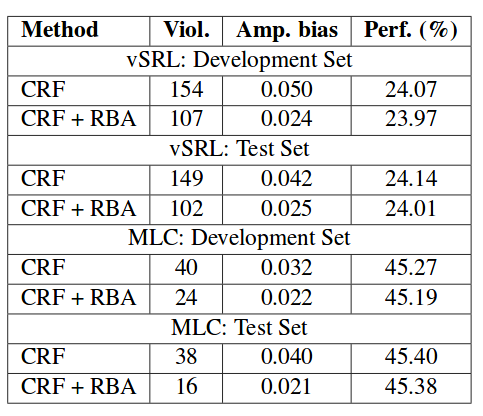
—– Team Gibbon: Austin Chen, Jin Ding, Ethan Lowman, Aditi Narvekar, Suya
References
[1] Till Speicher, Muhammad Ali, Giridhari Venkatadri, Filipe Nunes Ribeiro, George Arvanitakis, Fabrício Benevenuto, Krishna P. Gummadi, Patrick Loiseau, Alan Mislove. “Potential for Discrimination in Online Targeted Advertising.” Proceedings of the 1st Conference on Fairness, Accountability and Transparency, PMLR 81:5-19, 2018.
[2] Anupam Datta, Shayak Sen, Yair Zick. “Algorithmic Transparency via Quantitative Input Influence: Theory and Experiments with Learning Systems.” 2016 IEEE Symposium on Security and Privacy (SP), 2016.
[3] Aylin Caliskan, Joanna J. Bryson, Arvind Narayanan. “Semantics derived automatically from language corpora contain human-like biases.” Science Magazine, 2017.
[4] Rush, Alexander M., and Michael Collins. “A tutorial on dual decomposition and Lagrangian relaxation for inference in natural language processing.” Journal of Artificial Intelligence Research (2012).
[5] Yatskar, Mark, Luke Zettlemoyer, and Ali Farhadi. “Situation recognition: Visual semantic role labeling for image understanding.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016.
[6] Baker, Collin F., Charles J. Fillmore, and John B. Lowe. “The berkeley framenet project.” Proceedings of the 17th international conference on Computational linguistics-Volume 1. Association for Computational Linguistics, 1998.
[7] Miller, George A., et al. “Introduction to WordNet: An on-line lexical database.” International journal of lexicography 3.4 (1990): 235-244.
[8] Lin, Tsung-Yi, et al. “Microsoft coco: Common objects in context.” European conference on computer vision. Springer, Cham, 2014.
[9] Andreou, Athanasios, et al. “Investigating ad transparency mechanisms in social media: A case study of Facebook’s explanations.” NDSS, 2018.
Class 6: Measuring Robustness of ML Models
Motivation
In what seems to be an endless back-and-forth between new adversarial attacks and new defenses against those attacks, we would like a means of formally verifying the robustness of machine learning algorithms to adversarial attacks. In the privacy domain, there is the idea of a differential privacy budget, which quantifies privacy over all possible attacks. In the following three papers, we see attempts at deriving an equivalent benchmark for security, one that will allow the evaluation of defenses against all possible attacks instead of just a specific one.
Provably Minimally Distorted Adversarial Examples
Nicholas Carlini, Guy Katz, Clark Barrett, David L. Dill. Provably Minimally-Distorted Adversarial Examples. arXiv preprint arXiv:1709.10207. September 2017.
Guy Katz, Clark Barrett, David Dill, Kyle Julian, Mykel Kochenderfer. Reluplex: An efficient SMT solver for verifying deep neural networks. International Conference on Computer Aided Verification. 2017. [PDF]
There have been many attacking techniques against deep learning models that can effectively generate adversarial examples, such as FGSM, JSMA, DeepFool and the Carlini & Wagner attacks. But most of them couldn’t verify the absence of adversarial examples even if they fail to find any result.
Researchers have started to borrow the idea and techniques from the program verification field to verify the robustness of neural networks. In order to verify the correctness of a program, we can encode a program into SAT-modulo-theories (SMT) formulas and use some off-the-shelf solvers (e.g. Microsoft Z3) to verify a correctness property. An SMT solver generates sound and complete results, either telling you the program never violates the property, or giving you some specific counter-examples. However, we may not be able to get the results for some large programs in our lifetime, because it is an NP-complete problem.
Similarly, the current neural network verification techniques haven’t been able to deal with deep learning models of arbitrary size. But one of the prototype named Reluplex has produced some promising results on the MNIST dataset.
The Reluplex is an extension of the Simplex algorithm. It introduces a new domain theory solver to take care of the ReLU activation function because the Simplex only deals with linear real arithmetic. You can find more details about Reluplex in:
Guy Katz, Clark Barrett, David Dill, Kyle Julian, Mykel Kochenderfer. Reluplex: An Efficient SMT Solver for Verifying Deep Neural Networks. Arxiv. 2017.
The paper we discuss here uses Reluplex to verify the local adversarial robustness of two MNIST classification models. We say a model is delta-locally-robust at input \(x\) if for every \(x’\) such that \( ||x-x'||p \le \delta \), the model predicts the same label for \(x\) and \(x’\). Local robustness is certified for individual inputs, which is substantially different from the global robustness that certifies the whole input space. The paper performs binary search on delta to find the minimal distortion at a certain precision, and each delta corresponds to one execution instance of Reluplex. The paper only considers the \(L_{infinity}\) norm and the \(L_1\) norm because it is easier to encode these constraints with Reluplex. For example, the \(L_1\) norm could be encoded as \( |x| = max(x, -x)=ReLu(2x)-x \).
The evaluation is conducted on a fully-connected, 3-layer network that has 20k weights and fewer than 100 hidden neurons. The testing accuracy of the model is 97%. The model is smaller than most of the state-of-the-art models and has inferior accuracy, but should be good enough for the model verification prototype. The authors arbitrarily selected 10 source images with known labels from the MNIST test set, which produced 90 targeted attack instances in total.
Even though the Reluplex method is faster than most of the existing general SMT solvers, it is not fast enough for verifying the MNIST classification models. For every configuration with different target models and different \(L_p\) norm constraints, Reluplex always timed out for some of the 90 instances. The experiments with the \(L_1\) constraint were generally slower than those with the L_infinity constraint, because it introduced more ReLU components. However, we still found some interesting results from the successful verification instances.
The paper compared the minimally-distorted adversarial examples found by Reluplex with those generated by the CW attack and concluded that iterative optimization-based attacks are effective because the CW attack produced adversarial examples within 12% of optimal on the specific models.
The paper also evaluated a particular defense technique proposed by Madry et al. which is an adversarial training method that uses the PGD attack and enlarges the model capacity. The paper concluded that the PGD-based adversarial training increased the robustness to adversarial examples by 4.2x on the examined samples. Even though this result doesn’t guarantee the efficacy at larger scale, it proves that the defense increases the robustness against all future attacks while it is only trained with the PGD attack.
Evaluating the Robustness of Neural Networks
Tsui-Wei Weng, Huan Zhang, Pin-Yu Chen, Jinfeng Yi, Dong Su, Yupeng Gao, Cho-Jui Hsieh, Luca Daniel. Evaluating the Robustness of Neural Networks: An Extreme Value Theory Approach. ICLR 2018. January 2018 [PDF]
Little work has been done towards developing a comprehensive measure of robustness for neural networks, primarily due to them growing mathematically complex as the number of layers increases. The authors contribute a lower bound on the minimal perturbation needed to generate an adversarial sample. They accomplish this by using the extreme value theorem to estimate the local Lipschitz constant for a given sample.
The work is motivated by the success of a particular attack by Carlini and Wagner against several previous defense strategies such as defensive distillation, adversarial training, and model ensemble [2]. This highlights the need for a means for evaluating a defenses effectiveness against all attacks rather than just the ones tested against.
Previous attempts at deriving such a lower bound have shortcomings of their own. Szegedy et al. compute the product of the global Lipschitz constant of each layer of the network to derive a metric of instability of a deep neural network’s output; however the global Lipschitz constant is a loose bound [3].
Hein and Andriushchenko derived a closed-form bound using the local Lipschitz constant, but such a bound is only feasible for networks with one hidden layer. Several other approaches used linear programming to verify properties of neural networks, but they are also infeasible for large networks [4].
The most similar work uses a linear programming formulation to derive an upper bound on the minimum distortion needed, which is not as useful as a universal robustness metric, and also is infeasible for large networks due to the computational complexity of linear programming.
Robustness metric
In order to derive a formal robustness guarantee, the authors formulate the lower bound for the minimum adversarial distortion needed to be a successful perturbed example (success here meaning fooling the classifier, thus becoming adversarial). They accomplish this by relating p-norm of the perturbation \(\lVert \delta \rVert_p \) to the local Lipschitz constant \( L_q^j \), local meaning defined over a l-ball around the input They use properties of Lipschitz continuous functions to prove the following:
$$ \lVert \delta \rVert \le \min_{j \ne c} \frac{f_c(x_0) - f_j(x_0)}{L_q^j} $$
That is to say that if the the p-norm of the perturbation is less than the difference between any two classifications of the input, \((x_0\)), divided by the local Lipschitz constant.
The authors go on to provide a similar guarantee for networks where the activation function is not differentiable, for example an ReLU network. In such a case, the local Lipschitz constant can be replaced with the supremum of the directional derivatives for each direction heading towards the non-differentiable point.
CLEVER Robustness Metric
Since the above formulations of the lower bound are difficult to compute, the authors present a technique for estimating the lower bound, which is much more feasible computationally. They make use of the extreme value theorem, which claims that for any random variable, the maximum value of infinite samples of it follows a known distribution. In this case, the random variable is the p-norm of the gradient of a given sample. The authors assume a Weibull non-degenerate distribution for this paper and verify it as a reasonable assumption empirically.
To apply the theorem, they generate N samples in a ball around a given sample and calculate the gradient norm of each sample. Using the maximum value of the gradient over those N samples, they apply maximum likelihood to get distribution parameters that maximize the probability of those gradients. It should be noted that this approach assumes that the adversarial examples are well-distributed enough that enough random noise will generate them.
The resulting CLEVER score is an approximate lower bound on the distortion needed for an attack to succeed.
Experiments and Results
To evaluate how effective an indicator of robustness the CLEVER score is, the authors conducted experiments using the CIFAR-10, MNIST, and ImageNet data sets, pairing each data set with a set of neural network architectures and corresponding popular defenses for those networks.
They estimate the Weibull distribution parameter and conduct a goodness-of-fit test to verify that the distribution fits the data empirically.
They then apply two recent state-of-the-art attacks to their models, the Carlini and Wagner attack [2], covered in a previous blog post, and I-FGSM [3]
To evaluate the CLEVER score’s effectiveness, the authors compare it with the average \( L_2 \) and L_infinity distortions for each adversarial example generated by each type of attack. Since the score is an estimate of the lower bound of the minimal distortion needed, if it is an accurate estimate, then no attack should succeed with a distortion less than the lower bound. Their results show that this holds under both distortion metrics.
These results also show that the Carlini Wagner attack produces adversarial examples with distortion much closer to minimal than I-FGSM, which demonstrates the CLEVER score’s ability to evaluate the strength of attacks themselves. The score also serves as a metric for the effectiveness of of defenses against adversarial attacks since the score was shown to increase for defensively distilled networks. The authors generally contribute a means of providing theoretical guarantees about neural networks that is no limited by the size of the network.
However, there does not seem to be a correlation between the CLEVER score and the distortion needed by the Carlini Wagner attack. If the score were to truly indicate how hard it is to generate adversarial examples, then we would expect that networks with a higher CLEVER score to have higher average distortions than networks with lower scores, but this was not always the case.
Lower bounds on the Robustness to Adversarial Perturbations
Jonathan Peck, Joris Roels, Bart Goossens, Yvan Saeys Lower bounds on the robustness to adversarial perturbations. NIPS 2017.
In this paper, the authors propose theoretical lower bounds on the adversarial perturbations on different types of layers in neural networks. They then combine these theoretical lower bounds derived layer-by-layer, and apply it to the entire network to calculate the theoretical lower bound for adversarial perturbations for the network. In contrast to previous work on this topic, the authors derive the lower bounds directly in terms of the model parameters. This is useful for applying the bounds on real-world DNN models.
Lower bounds on different classifiers
The authors use a modular approach to find the lower bound of a feedforward neural network. In this approach, they derive the lower bound at a particular layer by working their way backward starting from the output layer, and gradually towards the input layer. More precisely, given a layer that takes as input \(y\) and computes a function \(h\) on the input, if we know the robustness bound of the following layer \(k\), then the goal at the current layer is to find the perturbation \(r\) such that,
$$||h(y+r)|| = ||h(y)|| + k$$
Any adversarial perturbation to that layer, \(q\) is guaranteed to satisfy \(||q|| \geq ||r||\).
The lower bounds for different types of layers, as proposed in the paper, is shown below. The proofs can be found in the supplemental materials provided by the authors of the paper.
Softmax output layers
Let \(r\) be the smallest perturbations to the input \(x\) of a softmax layer such that \(f(x+r) \neq f(x)\). The authors have shown that this condition is then satisfied:
Fully connected layers
Here, the assumption is that the next layer has a robustness of \(k\). In that case, the authors have shown that the minimum perturbations \(r\) satisfies this condition:
Here, \(J(x)\) is the Jacobian matrix of \(h_L\) at \(x\), and \(M\) is the bound of the second order derivative of \(h_L\).
Convolutional layers
For a convolutional layer with filter tensor \(W \in R^{k \times c \times q \times q}\), and input tensor \(X\), the adversarial perturbation \(R\) satisfies this condition:
Pooling layers
For a MAX or average pooling layer, the adversarial perturbation \(R\) satisfies:
And for \(L_p\) pooling:
Results
The authors conducted their experiments using the MNIST and CIFAR-10 datasets on the LeNet network. For generating the adversarial perturbations for testing the theoretical bounds, they used the fast gradient sign method (FGSM). They used a binary search to find the smallest perturbation parameter of FGSM that resulted in misclassification of a sample.
In their experiments, the authors did not find any adversarial sample that violated the theoretical lower bounds. The experimental and theoretical perturbation norms can be seen in the following two tables:
It can be seen that the mean theoretical perturbation is much lower than the experimental ones for both MNIST and CIFAR-10 datasets. The authors suggest this is due to FGSM not being the most efficient attacking technique.
In conclusion, the authors suggest it is still unclear how tight these theoretical bounds are. It will be interesting to verify how close they are to the minimal distortion achieved by more efficient attacking techniques. Moreover, they have only tried their method on feedforward networks. Applying it to recurrent networks is a possible future direction. Finally, they propose the adoption of a precise characterization of networks in terms of tradeoff between robustness and accuracy.
— Team Bus:
Anant Kharkar,
Atallah Hezbor,
Bhuvanesh Murali,
Mainuddin Jonas,
Weilin Xu
References
[1] T.-W Weng, H. Zhang, P.-Y. Chen, J. Yi, D. Su, Y. Gao, C.-J. Hsieh, L. Daniel “Evaluating the robustness of neural networks: An extreme value theory approach” ICLR 2018, January 2018.
[2] N. Carlini, D. Wagner “Towards evaluating the robustness of neural networks” arXiv preprint arXiv:1608.04644, March 2017.
[3] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, R. Fergus. “Intriguing properties of neural networks” arXiv preprint arXiv:1312.6199, 2013.
[4] M. Hein, M. Andriushchenko. “Formal guarantees on the robustness of a classifier against adversarial manipulation” arXiv preprint arXiv:1705.08475, 2017.
[5] I.J. Goodfellow, J. Shlens, C. Szegedy. “Explaining and harnessing adversarial examples” arXiv preprint arXiv:1412.6572, March 2015.
[6] Nicholas Carlini, Guy Katz, Clark Barrett, David L. Dill “Provably Minimally-Distorted Adversarial Examples” arXiv preprint arXiv:1709.10207, February 2018.
[7] Guy Katz, Clark Barrett, David Dill, Kyle Julian, Mykel Kochenderfer “Reluplex: An efficient SMT solver for verifying deep neural networks.” International Conference on Computer Aided Verification. Springer, Cham, 2017.
Class 5: Adversarial Machine Learning in Non-Image Domains
Beyond Images
While the bulk of adversarial machine learning work has focused on image classification, ML is being used for a vartiety of tasks in the real world and attacks (and defenses) for different domains need to be tailored to the purpose of the ML process. Among the most significant uses of ML are natural language processing and voice recognition. Within these fields, attacks look very different from those on images. With images, individual pixels can be changed large amounts without making the image unrecognizable, whereas in voice recognition, the audio needs to remain smooth, but many transformations can be done that are not noticable to humans. These attacks are becoming more and more significant as always active listening devices like Amazon Alexa are becoming more common in the public sector. A broadcast television attack could be used to access personal accounts and devices of thousands of people simultaneously without many of those being attacked even noticing.
Adversarial Audio
Nicholas Carlini and David Wagner. Audio Adversarial Examples: Targeted Attacks on Speech-to-Text. University of California, Berkeley. 5 January 2018. [PDF]
If classic science fiction authors, painting grandiose visions of artificial intelligence in the future, could read some of the tech headlines of today, they might be surprised by how their predictions panned out:
These news articles recount recent incidents in which smart home voice-controlled devices have been activated by voices in television advertisements and shows, rather than from a physically-present human voice. While these untargeted, accidental (we assume) occurrences perhaps make for amusing news, they reflect a significant potential vulnerability in speech-to-text systems against targeted, adversarial attacks.
In their 2018 paper, authors Carlini and Wagner develop and demonstrate a white-box attack against automated speech recognition systems: “given any audio waveform, we can produce another that is over 99.9% similar, but transcribes as any phrase of choice”. That is, a virtually unaltered sample, which might sound, at worst, noisy or mildly distorted to human ears, will be translated as an entirely different set of characters by the system.
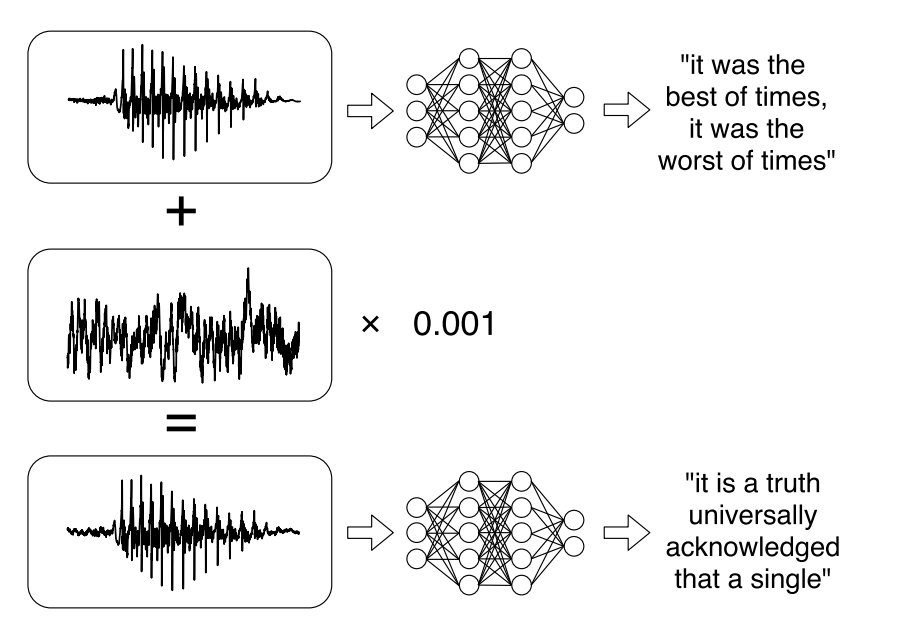
Audio distortion
The goal of this attack is twofold: (a) to add the least possible amount of distortion to the original audio, and (b) to cause the distorted audio to map to an arbitrary sequence of transcribed characters. This thus becomes an optimization problem.
To measure distortion, we use \(dB(v)\) to represent the loudness of a given sample \(v\) measured in decibels. First, let the change between the original and distorted samples be
$$dB_x(\delta) := dB(\delta) - dB(x)$$
where \(x\) is original and \(\delta\) distorted. Then, let
$$C(v) = \mathop{\arg,\max}\limits_p Pr[p | f(v)]$$
be the most likely transcribed phrase given some sample \(v\).
Our optimization problem becomes thus:
$$\text{minimize } dB_x(\delta)$$ $$\text{such that } C(x+\delta)=t$$ $$\text{with } x+\delta \in [-M,M]$$
where \(t\) is the target transcribed phrase and \(M\) is the maximum representable value (no distorted samples that are out of range – in the authors’ case, this happens to be \(2^{15}\) dB)).
However, due to the nonlinearity of \(C(\cdot)\), gradient descent fails, so instead we minimize
$$dB_x(\delta) + C(\cdot) \cdot \ell(x+\delta,t)$$ $$\text{with } \ell(x’,t) = \text{CTC-Loss}(x’,t)$$
where the \(\text{CTC-Loss}\) (Connectionist Temporal Classification Loss) function is just the negative log-likelihood function.
After solving this optimization problem, the authors constructed targeted examples on the first 100 test instances of Mozilla’s Common Voice dataset, attempting to distort 10 of these to achieve 10 target incorrect transcriptions – with 100% success for source-target pairs, and a mean perturbation magnititude of -31 dB.
Even after changing the loss function to
$$\ell(x,pi) = \sum_i \max (f(x)^i_{\pi^i}-\max_{t’\neq \pi^i} f(x)^i_{t’},0) $$
which avoids reducing loss and forces it to be more strongly classified, the mean distortion was only reduced from -31 dB to -38 dB, still a barely-noticeable to unnoticeable change.
Attack Sources and Targets
Attack models worked consistently regardless of context, meaning that an attack using white noise or non-speech is as easy to craft as one using speech. Targeting silence turned out to be even easier than targeting speech.
Robustness
Random pointwise noise of less than -30dB is sufficient to corrupt an attack; although stronger attacks can be crafted using larger dB changes. The attacks did manage to be MP3 resistent, which speaks to the minimization of loss in MP3 compression as well as the fidelity of the attack model.
These attacks do become easier with longer sources, as the pacing of the target speech can be varied more, giving a larger attack space in which to work. In an ideal case for an attacker, they would be working with a prerecorded broadcast, which gives them a large continuous space to attack. That said, Over-The-Air attacks were not viable due to the white noise and variation in speakers and the rooms. Hidden voice commands did, however, show some promise for broadcast attacks.
Transferability was shown to hold, as it is somewhat fundamental to ML systems. As of yet, defence techniques on the ML layers have not yet been developed, although random noise added post-attack is a viable defence.
Natural Language Processing
Suranjana Samanta and Sameep Mehta. Towards Crafting Text Adversarial Samples. 2017.
Adversarial samples are strategically modified samples, which are crafted with the purpose of fooling a classifier at hand. Although most of the prior works have been focused on synthesizing adversarial samples in the image domain, NLP based text classifiers can also be the focal point of such exploit. This paper introduces a method of crafting adversarial text samples by modification of the original samples. To be precise, the authors propose to modify the original text samples by deleting or replacing the important words in the text or by introducing new words in the text sample. While crafting adversarial samples, the paper focuses on generating meaningful sentences which can pass off as legitimate from language viewpoint.
Approach
Initially, the authors calculate contribution of each word towards determining the class-label. A word in the text is highly contributing if its removal from the text is going to change the class probability value to a large extent. In their proposed approach, modification of the sample text by considering each word at a time, in the order of the ranking based on the class-contribution factor. For the modification purpose, a candidate pool for each word in sample text is created considering synonyms and typos of each of the words as well as the genre or sub-category specific keywords. The assumption behind choosing sub-category or genre-specific keywords based on the fact that certain words may contribute to positive sentiment for a particular genre but can emphasis negative sentiment for other kind of genre. For example, we can consider the sentence, “The movie was hilarious”. This indicates a positive sentiment for a comedy movie. But the same sentence denotes a negative sentiment for a horror movie. Thus, the word ‘hilarious’ contributes to the sentiment of the review based on the genre of the movie. Finally, replacement, addition or removal of words are performed on a given text sample at each iteration, so that the modified sample flips its class label.
Experiments
The paper performs their experimental results on two datasets: IMDB movie review dataset for sentiment analysis and twitter dataset for gender classification. They compare the efficiency of their method with the existing method TextFool by measuring the accuracy of the model obtained at different configurations. For both the cases, the proposed model was generated using Convolutional Neural Network (CNN).
The figure below (taken from the paper) shows the results for IMDB dataset. From the figure, it is obvious that the proposed method of adversarial sample crafting for text is capable of synthesizing semantically correct adversarial text samples from the original text sample. In addition, the inclusion of genre specific keywords appears to increase the quality of sample crafting. This is evident from the fact the drop in accuracy of the classifier before re-training for original text sample and the adversarialy crafted text sample is more when genre specific keywords are being used.
A significant factor for evaluating the effectiveness of adversarial samples is to measure the semantic similarity between the original samples and their corresponding tainted counterparts. A lower similarity score denotes that the semantic meaning of the original and the modified samples are quite different, which is not acceptable from the language viewpoint. The authors found the average semantic similarity between the original text sample and their adversarial counterparts (for test set only) as 0.9164 and 0.9732 with and without using the genre specific keywords respectively. Although the semantic similarity between the original and their corresponding perturbed samples does decrease a bit while the genre specific keywords in the candidate pool, the number of valid adversarial samples generated increases as it can be seen from the percentage of the perturbed samples for genre specific keywords in the above figure.
Another key component for the evaluation of adversarial samples is to measure the number of changes incurred to obtain the adversarial sample. The number of changes made to craft a successful adversarial sample should be ideally low.The following figure shows a graph that indicates the number of changes required to create successful adversarial samples with and without using the genre-specific keywords. From the figure, it is evident that, if we consider same number of modifications the number of tainted sample produced using genre specific keywords for creating adversarial samples is more than that when genre specific keywords are not used.
For the Twitter dataset, the proposed method shows similar performance as the IMDB dataset.
Example
Face Recognition
Mahmood Sharif, Sruti Bhagavatula, Lujo Bauer, Michael K. Reiter. Accessorize to a Crime: Real and Stealthy Attacks on State-of-the-Art Face Recognition. ACM CCS 2016.
Face recognition and face detection algorithms are extensively used in surveillance and access control applications. This paper focuses on fooling the state-of-art machine learning algorithms that are practically deployed for these tasks. More concretely, the paper carries out two types of attacks: dodging and impersonation. In dodging, the attacker tries to conceal his/her identity, whereas, in impersonation, the attacker tries to trick the algorithm into recognizing him/her as a different target individual. The authors realize these attacks by printing a wearable glass which, upon wearing, allows the attacker to successfully launch the attacks. The glasses used in the attack are shown below.
Parikh et al. proposed the state-of-art 39 layer deep neural network trained on 2,622 celebrities which achieved an accuracy of 98.95% for the task of face detection. The authors of this paper use this model to launch their attacks.
The objective function of the deep neural network’s softmax layer is given as below:
For impersonation, the objective is to add the minimum amount of noise \(r\) in the input image \(x\) to convert the class lable to the target label \(c_t\), as given below:
For dodging, the objective is to add minimum amount of noise \(r\) in the input image \(x\) to deviate from the correct class label \(c_x\).
The noises are then carefully added to the 3D printed glasses.
Experiments
The paper launches successful dodging and impersonation attacks. Figure below shows an example of impersonation where a female celebrity (left) is classified as a male celebrity (right) by the algorithm when the glass frame is used (center).
Figure below shows an example of dodging the face detection algorithm with minor changes to the image that donot affect a normal human judgement. Left image is the original image and the center and right images are the perturbed images where the algorithm does not detect the faces.
Further results show 100% dodging success rate and very high impersonation success rate.
Summary
While the authors perform white-box attacks on the state-of-the-art face detection and face recognition algorithms, they also discuss about successfully carrying out the black-box attacks.
— Team Nematode: \
Bargav Jayaraman, Guy “Jack” Verrier, Joshua Holtzman, Max Naylor, Nan Yang, Tanmoy Sen
References
[1] Nicholas Carlini and David Wagner, “Audio Adversarial Examples: Targeted Attacks on Speech-to-Text.” January 2018.
[2] Mahmood Sharif, Sruti Bhagavatula, Lujo Bauer, and Michael K. Reiter, “Accessorize to a Crime: Real and Stealthy Attacks on State-of-the-Art Face Recognition.” October 2016.
Class 4: Differential Privacy In Action
Two weeks ago we took a look at privacy in machine learning and introduced differential privacy as one possible approach to perform statistical analysis on data while maintaining user privacy. Today we explore three applications of differential privacy: Google’s RAPPOR for obtaining user data from client-side software, the FLEX system to enforce differential privacy for SQL queries, and an algorithm for training deep neural networks that can provide differential privacy guarantees.
Google’s RAPPOR
Erlingsson, Úlfar, Vasyl Pihur, and Aleksandra Korolova. Rappor: Randomized aggregatable privacy-preserving ordinal response. ACM CCS 2014. [PDF]
The goal of Randomized Aggregatable Privacy-Preserving Ordinal Response (RAPPOR) is to ensure anonymity for those participating in crowd-sourced statistics with a strong privacy guarantee. For example, if student who has cheated is participating in a study on cheating in school it is unlikely they would respond truthfully without strong plausible deniability.
A simple algorithm that constructs such plausible deniability is shown below:
STEP ONE
flip coin
if (coin==HEADS):
answer truthfully
else:
go to step 2
STEP TWO
flip coin
if (coin==HEADS):
answer yes
else:
answer truthfully
This algorithm will result in a truthful response rate of 75%. Therefore if we let \(Y = [\text{Number of raised hands}] / [\text{Size of class}]\) then \([\text{Number of true cheaters}] \approx 2(Y − 0.25)\).
This means we have differential privacy with the level \(\epsilon = \ln(0.75/(1 − 0.75)) = \ln(3)\), but only for the first time responses are collected. This guarantee degrades if the same survey is administered repeatedly (where the same respondants generate new randomness for each query). RAPPOR is a way to ensure strong privacy protection even for a single respondent who is surveyed often.
On a high level, RAPPOR achieves this by having each client machine report a “noisy” representation of the true value \(v\) by submitting a \(k\)-sized bit array to a server. This representation of \(v\) is selected in order to reveal a specific amount of information about \(v\) in order to limit the information the server learns from the \(k\)-sized bit array. Importantly the server does not learn the true value \(v\) with confidence even when an infinite number of reports are submitted by the client.
This is achieved through the the following three steps:
- Signal - hash the client’s value \(v\) onto the Bloom filter \(B\) of size \(k\) using \(h\) hash functions.
A Bloom filter is a probabilistic data structure optimized for determining set membership.
- Permanent Randomized Response For each value \(v\) from a client, and for each bit \(i\) in the bloom filter \(B\), create a binary reporting value \(B_i’\) such that TODO:missing equation here??? where \(f\) is a user-defined tuning variable, \(f \in (0,1)\). This \(B’\) is memorized and reused as the basis for all future reports on value \(v\).
- Instantaneous Randomized Response. Next, allocate a bit array \(S\) of size \(k\) and initialize to 0. Set each bit \(i\) in \(S\) with the following probabilities: TODO:???
- Report. Send the bit array \(S\) to the server.
How private are RAPPOR’s aggregated results in reality? If you assume infinite sampling, there is a privacy guarantee of:
An attacker with “unlimited collection capabilities… is also bounded by the privacy guarantee of ε∞ and cannot improve upon this bound with more data collection.”
Towards Practical Differential Privacy for SQL Queries
Johnson, Noah, Joseph P. Near, and Dawn Song. Towards Practical Differential Privacy for SQL Queries. Proceedings of the VLDB Endowment, January 2018. [PDF] (Images below are taken from this paper.)
Motivation
The recent increase in data collection in large organizations has exposed personal user data to analysis that have an impact on user privacy. This paper investigates the methods that can be used to increase differential privacy, protecting individual privacy. By taking a practical approach to differential privacy, the authors are able to provide an implementation of differential privacy that is compatible with any existing database.
Contributions
- Empirical study of 8.1 million real-world SQL queries
- Elastic sensitivity
- FLEX: An end-to-end differential privacy system
- Experimental evaluation of FLEX
Elastic sensitivity
Elastic sensitivity is the paper’s main contribution and proposed approach to enforcing differential privacy on a system that is locally sensitivity-based. Local sensitivity is the “maximum of the difference between the query run on a true database and any neighbor of it.” The practical nature of their design exists because instead of being a property of all possible databases, local sensitivity is a property of one true database.
Limitation of existing approaches
Two main requirements of differential privacy are stated. The first is that the implementation of differential privacy must be compatible with existing databases, and have support for heterogeneous databases. Also it should have robust support for equijoins, which include self and non-self joins, relationship types and an arbitrary number of nested joins.
As seen in the chart above, other approaches address parts of the requirements, and elastic sensitivity seems to cover all of the requirements set forth in this paper for differential privacy. One lacking requirement among previous approaches was adequate database compatibility.
Unsupported Queries and other aggregate functions
Since non-equijoins need information about both datasets, the operation is not supported in elastic sensitivity. Elastic sensitivity also sometimes fails to provide support for max-frequency metrics. However, not having support for either of these operations does not impact a majority of operations in either case.
FLEX
FLEX is an implementation of elastic sensitivity that is highly compatible with existing databases. The FLEX database structure is shown in the figure above. TODO: this is the wrong figure
By targeting support for specific SQL queries, their system can enforce differential privacy on most real world queries to databases. For a given SQL query, FLEX calculates its elastic sensitivity given an analysis of the query. FLEX then applies smooth sensitivity to the elastic sensitivity and adds noise drawn from the Laplace distribution to the original query results.
- Elastic sensitivity for 76% of queries
- Large error for unsupported queries: 14.14%
- Parsing errors: 6.58%
Comparison with wPINQ
This paper moves towards more practical approaches of differential privacy in SQL queries by proposing elastic sensitivity. The concept of elastic sensitivity was then tested through their implementation in FLEX. A comparison of FLEX and wPINQ is shown in the figure above. Adoption of this method by Uber for internal data analytics demonstrates the potential of their approach for having a large impact on data privacy.
Deep learning with differential privacy
Martin Abadi, Andy Chu, Ian Goodfellow, H Brendan McMahan, Ilya Mironov, Kinal Talwar, and Li Zhang. Deep learning with differential privacy. ACM CCS 2016 [PDF] (All figures below are taken from this paper)
Differential Privacy Recap
Differential Privacy can be defined in terms of the application-specific concept of adjacent databases. Suppose, for adjacent databases where each training dataset contains a set of image-label pairs, we say that two of these sets are adjacent if one image-label pair is present in one training set while absent in the other. A randomized mechanism \( \mathcal{M}: D \rightarrow R\) with domain D and range R satisfies \( (\epsilon, \delta) \)-differential privacy if for any two adjacent inputs \( d,d'~\epsilon ~D\) and for any subset of outputs \( S \subseteq R\) it holds that
$$ Pr[\mathcal{M}(d) ~\epsilon ~\mathcal{S}] \leq \mathcal{e}^{\epsilon} Pr[\mathcal{M}(d’) ~\epsilon ~\mathcal{S}] + \delta $$
Authors used Dwork et al.[1] privacy definition of allowing the possibility that plain \( \epsilon \)-differential privacy is broken with probability \( \delta \) in their work.
Approach
Their proposed technique consists of three components: differentially private SGD (Stochastic Gradient Descent) Algorithm, Moments Accountant and Hyperparameter Tuning.
Differentially private SGD Algorithm
Algorithm 1 describes their method for training a model with parameters \( \theta \) by minimizing the loss function \( L(\theta) \). At each step of computing of SGD, they calculated the gradient \( \nabla \theta L(\theta, x_i)\) for a random subset then clip the \(L_2\) norm of each gradient. After that they computed the average and for ensuring the privacy they added noise in those. They took the opposite direction of this average noisy gradient. Finally, they ouput the model with the privacy loss.
Moments Accountant
Each lot is \( (\epsilon, \delta)\)-DP if we choose \(\sigma \) in Algorithm 1 as \( \sigma \) = \(\frac{\sqrt{ 2\log(\frac{1.5}{\delta})}} {\epsilon} \) for Gaussian noise. Thus, each step is \( \mathcal{O}((q \epsilon),q\delta) \)-DP over the dataset, where q = \( \frac{L}{N}\) is the sampling probability of a lot over the dataset and \(\epsilon \leq 1 \). The result in the literature which gives the best overall bound is the strong composition theorem [2]. Strong composition theorem does not take into account any particular noise distribution under consideration. Authors invent a stronger accounting method, which is the moments accountant. In Algorithm 1, over \(T\) iterations, naive composition gives the bound of \( \mathcal{O}((qT \epsilon),qT\delta) \)-DP. Over \(T\) iterations, strong composition gives the bound of \( \mathcal{O}((q \epsilon \sqrt{T \log \frac{1}{\delta}}),qT\delta) \)-DP. Whereas, over \(T\) iterations, moments accountant gives a tighter bound of \( \mathcal{O}((q \epsilon \sqrt{T}),\delta) \)-DP.
Theorem: There exist constants \(c_1\) and \(c_2\) so that given the sampling probability q = L/N and the number of steps T, for any \( \epsilon < c_1q^{2}T \), Algorithm 1 is \( (\epsilon,\delta) \)-differentially private for any \(\delta > 0\) if we choose $$ \sigma \geq c_2 \frac{q \sqrt{T\log(\frac{1}{\delta})}}{\epsilon} $$
If we use the strong composition theorem, we will then need to choose \( \sigma = \Omega(q\sqrt{T\log(1/\delta)\log(T/\delta)}/\epsilon)\) For \(L = 0.01N\), \(\sigma\) = 4, \(\delta\) = \(10^{-5}\), and \(T = 10000\), we have \(\epsilon\) ≈ 1.26 using the moments accountant, and \(\epsilon\) ≈ 9.34 using the strong composition theorem.
Hyperparameter Tuning
Authors used the insight from the version of a result from Gupta et al. [3] restated as Theorem D.1 in the Appendix to reduce the number of hyperparameter settings. From theorem 1, one can say that making batches size too large will increase the privacy cost. The learning rate in non-private training will also go downwards as the model will converge to a local optimum. But authors found that they didn’t have to decrease the learning rate to a very small value because differentially private training never goes to an area where it would be justified. Moreover, from their experiment they came to know that there was a small advantage of starting with a large learning rate compare to small learning rate and then linearly decaying it to a smaller value in a few epochs. And after that the rate remained constant.
Implementation
They have implemented the differentially private SGD algorithms in TensorFlow. They made their code available to download under an Apache 2.0 license from github.com/tensorflow/models. Their whole implementation is divided into two components. One is Sanitizer which preprocesses the gradient to protect privacy and the other one is privacy accountant which keeps track of the privacy cost of training the model. They implemented differentially private PCA(Principal Directions) and applied pre-trained convolutional layers. Because the neural network model may benefit by projecting the inputs on the PCA or by feeding it through a convolutional layer.
Sanitizer
For achieving the privacy protection, the sanitizer performs the following two operations:
- Limits sensitivity of each example by clipping the norm of the gradient
- Adds noise to the gradient of a batch before updating network parameters
Privacy Accountant
The main purpose of their implementation is to keep track of privacy spending over the course of training and hence the implementation of Privacy Accountant is the most important component of their implementation. One can compute \(\alpha (\gamma)\) by two ways. First one is by applying asymptotic bound and then evaluating a closed-form expression and the second one is by applying numerical integration. In their implementation they used the second one to compute \(\alpha (\gamma)\). They also \(\alpha (\gamma)\) computed for a wide range of \( \gamma’s\), which helped them to get the best result possible \( (\epsilon, \delta) \) values. They stated that for the parameters it is enough to calculate \(\alpha (\gamma)\) where \(\gamma \leq 32\).
The above figure contains the TensorFlow code snippet (in Python) of DPSGD_Optimizer which iteratively invokes DPSGD_Optimizer using a privacy accountant to bound the total privacy loss.
Differentially private PCA
Differentially Private Principal Component Analysis is a very useful method for capturing the features of the input data. Authors implemented the differentially private PCA algorithm according to Dwork et al.[4]. They took a random sample from the training examples and treated them as vectors. They normalized each vector to unit \(l_2\) norm to form the matrix \(A^{T}A\). After that they added Gaussian noise to the matrix A. Then for each input example they applied the projection to the principal directions of noisy covariance matrix before feeding them into the neural network.
Experimental Results
MNIST
Figure: Results on the accuracy for different noise levels on the MNIST dataset. In all the experiments, the network uses 60 dimension PCA projection, 1,000 hidden units, and is trained using lot size 600 and clipping threshold 4. The noise levels \(\sigma, \sigma_{p}\) for training the neural network and for PCA projection are set at (8, 16), (4, 7), and (2, 4), respectively, for the three experiments.
In the above Figure, they showed the results for different noise levels. In each plot, they showed the evolution of the training and testing accuracy as a function of the number of epochs as well as the corresponding \(\delta\) value, keeping \(\epsilon\) fixed.
Figure: Accuracy of various \( (\epsilon,\delta) \) privacy values on the MNIST dataset. Each curve corresponds to a different \(\delta \) value.
In the above figure, they showed the accuracy that they can obtain for different value of \(\delta\) and \(\epsilon\). From the figure, one can observe that keeping the value of \(\delta\) fixed and varying the value of \(\epsilon\) can have large impact on the accuracy.
Figure: MNIST accuracy when one parameter varies, and the others are fixed at reference values.
In the above figure, they showed the accuracy of the model on MNIST dataset by by varying a particular parameter while keeping the other parameter constant. For training the neural network parameters and for PCA projection they set the reference values like - 60 PCA dimenstions, 600 lot size, 1000 hidden units, initial learning rate of 0.1, final learning rate 0.052 in 10 epochs, gradient norm bound of 4, and noise equal to 4 and 7 respectively.
CIFAR-10
Figure: Results on accuracy for different noise levels on CIFAR-10. With \(\delta \) set to \(10^{-5}\) , achieve accuracy 67%, 70%, and 73%, with \(\epsilon \) being 2, 4, and 8, respectively. The first graph uses a lot size of 2,000, (2) and (3) use a lot size of 4,000. In all cases, \(\sigma \) is set to 6, and clipping is set to 3.
In the above figure, authors showed the result of the accuracy and privacy cost of the model on the CIFAR-10 dataset as a function of the number of epochs for different parameter settings. In MNIST dataset, the difference in accuracy between a non-private baseline and a private model is about 1.3% whereas the corresponding drop in accuracy in CIFAR-10 dataset is about 7%.
— Team Panda Christopher Geier, Faysal Hossain Shezan, Helen Simecek, Lawrence Hook, Nishant Jha
References
[1] C. Dwork, K. Kenthapadi, F. McSherry, I. Mironov,and M. Naor. Our data, ourselves: Privacy via distributed noise generation. In EUROCRYPT, pages 486–503. Springer, 2006.\
[2] C. Dwork, G. N. Rothblum, and S. Vadhan. Boosting and differential privacy. In FOCS, pages 51–60. IEEE, 2010.\
[3] A. Gupta, K. Ligett, F. McSherry, A. Roth, and K. Talwar. Differentially private combinatorial optimization. In SODA, pages 1106–1125, 2010.\
[4] C. Dwork, K. Talwar, A. Thakurta, and L. Zhang. Analyze Gauss: Optimal bounds for privacy-preserving principal component analysis. In STOC, pages 11–20. ACM, 2014.\
To help with topics for future classes, I’ve created a Topics page with some possible ideas and links to papers. This is not meant to be exhaustive by any stretch; any topics loosely connected to machine learning security and privacy is within scope, and there are lots of great papers on these topics not included on this page. But, hopefully it will be a useful starting point for teams looking for ideas for topics for future classes.